question_answer

A variable line ?L? is drawn through \[O(0,\,\,0)\] to meet the lines \[{{L}_{1}}:y-x-10=0\] and \[{{L}_{2}}:y-x-20=0\] at the points A and B respectively. A point P is taken on ?L? such that\[\frac{2}{OP}=\frac{1}{OA}+\frac{1}{OB}.\] Locus of ?P? is

A) \[3x+3y=40\]

B) \[3x+3y+40=0\]

C) \[3x-3y=40\]     

D) \[3y-3x=40\]

Correct Answer: D

Solution :

[d] Let the parametric equation of drawn line

\[\frac{x}{\cos \theta }=\frac{y}{\sin \theta }=r\Rightarrow x=r\cos \theta ,y=r\sin \theta \]

Putting it in\['{{L}_{1}}'\], we get

\[r\sin \theta =r\,cos\theta +10\]

\[\Rightarrow \frac{1}{OA}=\frac{\sin \theta -\cos \theta }{10}\]

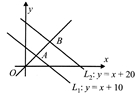Similarly, putting the

general point of drawn

line is the equation of \[{{L}_{2}},\]

we get

\[\frac{1}{OB}=\frac{\sin \theta -\cos \theta }{20}\]

Let \[P=(h,k)\] and \[OP=r\]

\[\Rightarrow r\cos \theta =h,r\sin \theta =k,\] we have

\[\frac{2}{r}=\frac{\sin \theta -\cos \theta }{10}+\frac{\sin \theta -\cos \theta }{20}\]

\[\Rightarrow 40=3r\sin \theta -3r\cos \theta \Rightarrow 3y-3x=40.\]