question_answer

Let \[P=(-1,0),Q=(0,0)\] and \[R=(3,3\sqrt{3})\] be three point. The equation of the bisector of the angle PQR is

A) \[\frac{\sqrt{3}}{2}x+y=0\]

B) \[x+\sqrt{3y}=0\]

C) \[\sqrt{3}x+y=0\]

D) \[x+\frac{\sqrt{3}}{2}y=0\]

Correct Answer: C

Solution :

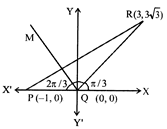
[c] The coordinates of points P, Q, R are\[(-1,0)\],\[(0,0)\], \[(3,3\sqrt{3})\], respectively.

Slope of QR

\[=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\frac{3\sqrt{3}}{3}\]

\[\Rightarrow \tan \theta =\sqrt{3}\]

\[\Rightarrow \theta =\frac{\pi }{3}\Rightarrow \angle RQX=\frac{\pi }{3}\]

\[\therefore \angle RQP=\pi -\frac{\pi }{3}=\frac{2\pi }{3};\]

Let QM bisects the \[\angle PQR,\]

\[\therefore \] Slope of the line \[QM=\tan \frac{2\pi }{3}=-\sqrt{3}\]

\[\therefore \] Equation of line OM is \[(y-0)=-\sqrt{3}(x-0)\]

\[\Rightarrow y=-\sqrt{3}x\Rightarrow \sqrt{3}x+y=0\]