question_answer

Let \[{{\vec{r}}_{1}},{{\vec{r}}_{2}},{{\vec{r}}_{3}},.....{{\vec{r}}_{n}},\] be the position vectors of points \[{{P}_{1}},{{P}_{2}},{{P}_{3}},....,{{P}_{n}}\] relative to the origin O. If the vector equation \[{{a}_{1}}{{\vec{r}}_{1}}+{{a}_{2}}{{\vec{r}}_{2}}+....+{{a}_{n}}{{\vec{r}}_{n}}=0\] holds, then a similar equation will also hold w.r.t. to any other origin provided

A) \[{{a}_{1}}+{{a}_{2}}+....+{{a}_{n}}=n\]

B) \[{{a}_{1}}+{{a}_{2}}+....+{{a}_{n}}=1\]

C) \[{{a}_{1}}+{{a}_{2}}+....+{{a}_{n}}=0\]

D) \[{{a}_{1}}={{a}_{2}}={{a}_{3}}=....={{a}_{n}}=0\]

Correct Answer: C

Solution :

[c] Given \[{{a}_{1}}{{\vec{r}}_{1}}+{{a}_{2}}{{\vec{r}}_{2}}+.....+{{a}_{n}}{{\vec{r}}_{n}}=0\] Now \[\vec{a}+{{\vec{r}}_{1}}'={{\vec{r}}_{1}}\] and so on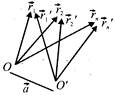 Hence, \[{{a}_{1}}(\vec{a}+{{\vec{r}}_{1}})+{{a}_{2}}(\vec{a}+{{\vec{r}}_{2}})+....+{{a}_{n}}(\vec{a}+{{\vec{r}}_{n}}')=0\] \[{{a}_{1}}{{\vec{r}}_{1}}'+{{a}_{2}}{{\vec{r}}_{2}}'+....+{{a}_{n}}{{\vec{r}}_{n}}'+\vec{a}({{a}_{1}}+{{a}_{2}}+....+{{a}_{n}})=0\] Hence, \[{{a}_{1}}{{\vec{r}}_{1}}'+{{a}_{2}}{{\vec{r}}_{2}}'+....+{{a}_{n}}{{\vec{r}}_{n}}'=0\] if \[{{a}_{1}}+{{a}_{2}}\]                                                 \[+....+{{a}_{n}}=0\].