question_answer

If \[\overset{\to }{\mathop{a}}\,,\text{ }\overset{\to }{\mathop{b}}\,,\text{ }\overset{\to }{\mathop{c}}\,\] are the position vectors of corners A, B, C of a parallelogram ABCD, then what is the position vector of the corner D?

A) \[\overset{\to }{\mathop{a}}\,+\overset{\to }{\mathop{b}}\,+\overset{\to }{\mathop{c}}\,\]

B) \[\overset{\to }{\mathop{a}}\,+\overset{\to }{\mathop{b}}\,-\overset{\to }{\mathop{c}}\,\]

C) \[\overset{\to }{\mathop{a}}\,-\overset{\to }{\mathop{b}}\,+\overset{\to }{\mathop{c}}\,\]

D) \[-\overset{\to }{\mathop{a}}\,+\overset{\to }{\mathop{b}}\,+\overset{\to }{\mathop{c}}\,\]

Correct Answer: C

Solution :

[c] Let O be the origin and ABCD be the parallelogram. In \[\Delta \,ODC,\] \[\overrightarrow{OD}=\overrightarrow{OC}+\overrightarrow{CD}\] \[\overrightarrow{CD}=-\overrightarrow{AB}\] and \[\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}\]                   [In \[\Delta \,AOB\]]                                                 \[=\overset{\to }{\mathop{b}}\,-\overset{\to }{\mathop{a}}\,\] Thus, \[\overrightarrow{CD}=-\overrightarrow{AB}=\overrightarrow{a}-\overrightarrow{b}\]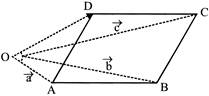 So, \[\overrightarrow{OD}=\overrightarrow{c}+\overrightarrow{a}-\overrightarrow{b}\] [since, \[\overrightarrow{OC}=\overrightarrow{C}\]and \[\overrightarrow{CD}=\overrightarrow{a}-\overrightarrow{b}\]]