question_answer

The components of a vector \[\vec{a}\] along and perpendicular to a non-zero vector \[\vec{b}\] are

A) \[\left( \frac{\vec{a}.\vec{b}}{{{\left| {\vec{b}} \right|}^{2}}} \right)\vec{b}\And \vec{a}-\left( \frac{\vec{a}.\vec{b}}{{{\left| {\vec{b}} \right|}^{2}}} \right)\vec{b}\]

B) \[\left( \frac{\vec{a}.\vec{b}}{{{\left| {\vec{a}} \right|}^{2}}} \right)\vec{b}\And \vec{a}+\left( \frac{\vec{a}.\vec{b}}{{{\left| {\vec{a}} \right|}^{2}}} \right)\vec{b}\]

C) \[\left( \frac{\vec{a}.\vec{b}}{{{\left| {\vec{a}} \right|}^{2}}} \right)\vec{a}-\left( \frac{\vec{a}.\vec{b}}{{{\left| {\vec{b}} \right|}^{2}}} \right)\vec{a}\]

D) None of these

Correct Answer: A

Solution :

[a] \[\overrightarrow{OM}=\] component

of \[\vec{a}\] along \[\vec{b}\]

\[\overrightarrow{MA}=\]component of \[\vec{a}\]

Perpendicular to \[\vec{b}\]

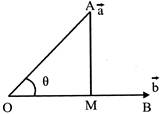\[\Delta \,OMA\Rightarrow \cos \theta =\frac{OM}{OA}\]

\[\Rightarrow \,\,OM=|\overrightarrow{OM}|=|\overrightarrow{OA}|cos\theta =|\vec{a}|cos\theta \]

\[\because \vec{a}.\vec{b}=|\vec{a}||\vec{b}|cos\theta =|\vec{b}|(OM)\]

\[\therefore \,\overrightarrow{OM}=|\overrightarrow{OM}|\hat{b}=\left( \frac{\vec{a}.\vec{b}}{|\vec{b}|} \right)\frac{{\vec{b}}}{|\vec{b}|}=\left( \frac{\vec{a}.\vec{b}}{|\vec{b}{{|}^{2}}} \right)\vec{b}\]

\[\overrightarrow{OM}+\overrightarrow{MA}=\overrightarrow{OA}\therefore \overrightarrow{MA}=\overrightarrow{OA}-\overrightarrow{OM}\]

\[=\vec{a}-\left( \frac{\vec{a}\cdot \vec{b}}{|\vec{b}{{|}^{2}}} \right)\vec{b}\]