10th Class Mathematics Sample Paper

done Maths Olympiad Model Test Paper-13 Total Questions - 40    [Download]

• question_answer1)
  Find the greatest numbers of 6 digits which is exactly divisible by 24, 15 and 36.
  A)
   99862             
  done clear
  B)
   98942
  done clear
  C)
   999720
  done clear
  D)
   999910
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer2)
  A circular field has a circumference of 360 km. Three cyclists start together and can cycle 48 km, 60 km and 72 km a day round the field, they will meet again at the same starting point after:
  A)
   32 days                       
  done clear
  B)
   28 days
  done clear
  C)
   30 days
  done clear
  D)
   35 days
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer3)
  If HCF and LCM of two numbers are 10 and 770 respectively, then the product of the two numbers is:
  A)
   77                               
  done clear
  B)
   770
  done clear
  C)
   7700   
  done clear
  D)
   15400
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer4)
  If one zero of the quadratic polynomial \[f\,\,\left( x \right)=4{{x}^{2}}-8kx-9\] is negative of the other, then find the value of k.
  A)
   0        
  done clear
  B)
   1
  done clear
  C)
   \[-\,1\]                         
  done clear
  D)
   2
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer5)
  If the square of difference of the zeroes of the polynomial \[f(x)={{x}^{2}}+px+45\] is equal to 144, then find the value of p.
  A)
   8                                
  done clear
  B)
   1
  done clear
  C)
   \[\pm \,9\]                                
  done clear
  D)
   \[\pm \,18\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer6)
  If \[\alpha \] and \[\beta \] are roots of the polynomial\[p(s)=3{{s}^{2}}-6s+4,\], then find the value of \[\frac{\alpha }{\beta }+\frac{\beta }{\alpha }+2\,\,\left( \frac{1}{\alpha }+\frac{1}{\beta } \right)+3\alpha \beta \].
  A)
   8
  done clear
  B)
   2
  done clear
  C)
   6                                
  done clear
  D)
   0
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer7)
  Find k such that \[3x+y=1\] and \[\left( 2k-\text{1} \right)\,\,x+\left( k-1 \right)\,\,y=2k+1\] has no solution.
  A)
   k = 3              
  done clear
  B)
   k = 2
  done clear
  C)
   k = 4              
  done clear
  D)
   k = 7
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer8)
  The sum of a two-digit number and the number formed by interchanging the digit is 132. If 12 is added to the number, the new number becomes 5 times the sum of the digits. Find the number.
  A)
   46                               
  done clear
  B)
   48
  done clear
  C)
   45                               
  done clear
  D)
   43
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer9)
  If 2 is a root of the equation \[{{x}^{2}}+bx+12=0\] and\[{{x}^{2}}+bx+k\] has equal roots, then k is equal to:
  A)
   8                                
  done clear
  B)
   16
  done clear
  C)
   \[-\,8\]                         
  done clear
  D)
   \[-\,16\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer10)
  A two digit number is such that the product of its digits is 18. When 63 is subtracted from the number, the digits interchange their places. Find the number.
  A)
   90                               
  done clear
  B)
   92
  done clear
  C)
   97                               
  done clear
  D)
   95
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer11)
  In a flight of 600 km, an aircraft was slowed down due to bad weather. Its average speed for the trip was reduced by 200 km/h and the time of flight increased by 30 minutes. Find the duration of flight.
  A)
   1 hour
  done clear
  B)
   5 hours
  done clear
  C)
   3 hours            
  done clear
  D)
   4 hours
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer12)
  In a garden-bed there are 23 rose plants in the first row, twenty-one in the second row, nineteen in the third row and so on. There are five plants in the last row. How many rows are there?
  A)
   10       
  done clear
  B)
   12
  done clear
  C)
   14                               
  done clear
  D)
   9
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer13)
  If \[\frac{{{a}^{n+1}}+{{b}^{n+1}}}{{{a}^{n}}+{{b}^{n}}}\] is the arithmetic mean between a and b, then find the value of n.
  A)
   1                                
  done clear
  B)
   2
  done clear
  C)
   0        
  done clear
  D)
   3
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer14)
  The sum of 4th and 8th term of an A.P. is 24 and sum of 6th and the 10th term is 44. Find the sum of first three terms of this A.P.
  A)
   8                                
  done clear
  B)
   \[-\,23\]
  done clear
  C)
   18                               
  done clear
  D)
   24
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer15)
  Find the curved surface area of a conical funnel whose volume is \[2079\text{ }c{{m}^{3}}\] and radius is 7 cm.
  A)
   \[594\,\,c{{m}^{2}}\]             
  done clear
  B)
   \[124\,\,c{{m}^{2}}\]
  done clear
  C)
   \[904.2\,\,c{{m}^{2}}\]
  done clear
  D)
   \[398.6\,\,c{{m}^{2}}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer16)
  Find the area of a hemispherical bowl whose outer radius is 12 cm and inner radius is 5 cm.
  A)
   \[216\,\,\pi \text{ }c{{m}^{2}}\]                      
  done clear
  B)
   \[238\,\,\pi \text{ }c{{m}^{2}}\]
  done clear
  C)
   \[248\,\,\pi \text{ }c{{m}^{2}}\]                      
  done clear
  D)
   \[264\,\,\pi \text{ }c{{m}^{2}}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer17)
  The length of a rectangular plot of land is two more than twice its breadth. If the perimeter of the plot is 64 m, then find its area.
  A)
   \[210\,\,{{m}^{2}}\]               
  done clear
  B)
   \[220\,\,{{m}^{2}}\]
  done clear
  C)
   \[230\,\,{{m}^{2}}\]               
  done clear
  D)
   \[240\,\,{{m}^{2}}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer18)
  It is given that \[\Delta \,ABC\sim \Delta \,PQR\] with \[\frac{BC}{QR}=\frac{1}{3}\]. Then \[\frac{ar\,(\Delta \,PRQ)}{ar\,(\Delta \,BCA)}\] is equal to:
  A)
   9        
  done clear
  B)
   3
  done clear
  C)
   \[\frac{1}{3}\]                         
  done clear
  D)
   \[\frac{1}{9}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer19)
  In \[\Delta \,ABC,\] PQ is a line segment intersecting AB at P and AC at Q such that \[PQ\parallel BC\] and PQ divides \[\Delta \,ABC\] into two parts equal in area, find \[\frac{BP}{AB}\].
  A)
   \[\frac{\sqrt{2-1}}{\sqrt{2}}\]                
  done clear
  B)
   \[\frac{1+\sqrt{3}}{2}\]
  done clear
  C)
   \[\frac{\sqrt{5+2}}{3}\]           
  done clear
  D)
   \[\frac{1+\sqrt{2}}{\sqrt{3}}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer20)
  Two circles touch externally at the point Q, and PR is the common tangent to the circle\[\angle PQR\] is equal to:
  A)
   \[60{}^\circ \]                         
  done clear
  B)
   \[45{}^\circ \]
  done clear
  C)
   \[90{}^\circ \] 
  done clear
  D)
   \[30{}^\circ \]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer21)
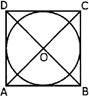
  Find the measure of \[\angle AOB\,\,\,+\angle COD\] from the figure given below if ABCD is a square.
  A)
   \[60{}^\circ \]                         
  done clear
  B)
   \[180{}^\circ \]
  done clear
  C)
   \[90{}^\circ \]                         
  done clear
  D)
   \[120{}^\circ \]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer22)
  If \[5\,\text{tan}\,\,q=4,\] then find the value of \[\frac{5\sin \theta -3\cos \theta }{5\sin \theta +2cos\theta }\]
  A)
   \[\frac{1}{3}\]                         
  done clear
  B)
   \[\frac{1}{2}\]
  done clear
  C)
   \[\frac{1}{6}\] 
  done clear
  D)
   \[\frac{2}{3}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer23)
  A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle of \[30{}^\circ \] with the ground. The distance between the foot of the tree to the point where the top touches the ground is 8 m. What is the height of the tree?
  A)
   \[8\,\sqrt{3}\,m\]
  done clear
  B)
   \[2\,\sqrt{5}\,m\]
  done clear
  C)
   \[5\,\sqrt{2}\,m\]                      
  done clear
  D)
   \[3\,\sqrt{2}\,m\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer24)
  Find the value of 'k' for which the points A (1, 2) B (3, k) and C (4, 5) are collinear.
  A)
   \[\frac{1}{2}\]                         
  done clear
  B)
   \[\frac{14}{3}\]
  done clear
  C)
   \[\frac{1}{3}\]                         
  done clear
  D)
   \[4\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer25)
  If A(4,2), B(a,0), C(6, b) and D(2,6) are the vertices of a parallelogram, then find the values of a and b.
  A)
   \[a=3,\,b=-\,3\]            
  done clear
  B)
   \[a=3,\,\,b=5\]
  done clear
  C)
   \[a\text{ }=1,\text{ }b=-\,3\]    
  done clear
  D)
   \[a=8,\text{ }b=4\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer26)
  Find the coordinate of centroid of a triangle ABC whose vertices are A (1, 2), B (0, 6) and C (3, 3).
  A)
   \[\left( \frac{4}{3},5 \right)\]                  
  done clear
  B)
   \[(0,3)\]
  done clear
  C)
   \[\left( 2,\frac{11}{3} \right)\]                 
  done clear
  D)
   \[\left( \frac{4}{3},\frac{11}{3} \right)\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer27)
  If the mode of a given data is 45 and mean is 27, then the median is:
  A)
   30                               
  done clear
  B)
   27
  done clear
  C)
   33       
  done clear
  D)
   41
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer28)
  The marks obtained out of 50, by 102 students is a Physics test are given in the frequency table below. Find the average number of marks.

  Marks (x)	15	20	22	24	25	30	33	38	45
  Frequency (f)	5	8	11	20	23	18	13	3	1

  A)
   25.5                            
  done clear
  B)
   27.2
  done clear
  C)
   25.98
  done clear
  D)
   22.57
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer29)
  A card is drawn from a well shuffled pack of 52 cards. The probability that the card is a black or a club is:
  A)
   \[\frac{1}{3}\]                         
  done clear
  B)
   \[\frac{1}{4}\]
  done clear
  C)
   \[\frac{1}{2}\]
  done clear
  D)
   \[\frac{3}{13}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer30)
  In a company there are 100 employees working in two different departments. They are in a group of 60 and 40 employees in the different departments. If there are 35% women in the company, then find the probability of selecting one woman for the post of manager.
  A)
  \[\frac{7}{20}\]                        
  done clear
  B)
  \[\frac{9}{20}\]
  done clear
  C)
  \[\frac{1}{5}\]                         
  done clear
  D)
  \[\frac{3}{5}\]
  done clear
  E)
  None of these
  done clear
  View Answer play_arrow

• question_answer31)
  Out of 15 boys and 12 girls in a class one student is to be chosen as a class monitor. Find the probability that the chosen student is a boy.
  A)
   \[\frac{7}{9}\]                         
  done clear
  B)
   \[\frac{2}{9}\]
  done clear
  C)
   \[\frac{1}{3}\]                         
  done clear
  D)
   \[\frac{5}{9}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer32)
  The sum and the product of zeros of a quadratic polynomial are \[\frac{9}{2}\] and 2 respectively. The quadratic polynomial is:
  A)
   \[{{x}^{2}}-9x+4\]                
  done clear
  B)
   \[2{{x}^{2}}-9x+4\]
  done clear
  C)
   \[{{x}^{2}}+9x+4\]              
  done clear
  D)
   \[2{{x}^{2}}+9x-2\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer33)
  If the sum of the zeros of the polynomial\[f(x)=({{k}^{2}}-14)\,{{x}^{2}}-2x-12,\] is 1, then one of the values of k is:
  A)
   \[\sqrt{14}\]                 
  done clear
  B)
   \[-\,14\]
  done clear
  C)
   \[2\]                            
  done clear
  D)
   \[-\,4\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer34)
  If and \[\alpha \],\[\beta \] are \[\gamma \] the zeroes of the polynomial\[p(x)=18{{x}^{3}}-15{{x}^{2}}-x+2,\] then the value of\[\frac{1}{\alpha \beta }+\frac{1}{\beta \gamma }+\frac{1}{\gamma \alpha }\] is:
  A)
   \[\frac{-15}{2}\]
  done clear
  B)
    \[\frac{1}{9}\]
  done clear
  C)
   \[-\frac{1}{18}\]                       
  done clear
  D)
   \[\frac{5}{6}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer35)
  Two ships are sailing in the sea on either side of a lighthouse. The angles of depression of the two ships are \[45{}^\circ \]each as observed from the top of the lighthouse. If the height of the lighthouse is 300 m, then the distance between the ships is:
  A)
   \[300\,m\]                    
  done clear
  B)
   \[300\,\sqrt{3}\,m\]
  done clear
  C)
   \[600\,m\]
  done clear
  D)
   \[\frac{600}{\sqrt{3}}\,\,m\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer36)
  A sphere and a cube have equal surface areas. Find the ratio of the volume of the sphere to that of the cube.
  A)
   \[\sqrt{\pi :}\sqrt{6}\]                
  done clear
  B)
   \[\sqrt{2}:\sqrt{\pi }\]
  done clear
  C)
   \[\sqrt{\pi }:\sqrt{3}\]                
  done clear
  D)
   \[\sqrt{6}:\sqrt{\pi }\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer37)
  If \[{{(5+2\sqrt{6})}^{{{x}^{2}}-3}}+{{(5-2\sqrt{6})}^{{{x}^{2}}-3}}=10,\] then x is equal to:
  A)
   \[2,2\]                          
  done clear
  B)
   \[\sqrt{2,}-\sqrt{2}\]
  done clear
  C)
   \[2,+\sqrt{2}\]             
  done clear
  D)
   \[2,-2,\sqrt{2},-\sqrt{2}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer38)
  Find the next number in the following sequence of numbers. 79, 83, 89, 97,101,103, ...
  A)
   105                             
  done clear
  B)
   107
  done clear
  C)
   108                             
  done clear
  D)
   109
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer39)
  Choose the figure which is different from the others.
  A)
                          
  done clear
  B)
   
  done clear
  C)
                        
  done clear
  D)
   
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer40)
  The salaries of A, B and C are in the ratio of 3 : 4 : 5 respectively. If the total of the salaries of A and B is Rs. 5250, what is the salary of C?
  A)
   Rs. 3000                      
  done clear
  B)
   Rs. 3750
  done clear
  C)
   Rs. 3700                      
  done clear
  D)
   Rs. 3500
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow