10th Class Mathematics Sample Paper

done Maths Olympiad Model Test Paper-5 Total Questions - 40    [Download]

• question_answer1)
  The length, breadth and height of a room are 8 m 25 cm, 6 m 75 cm and 4 m 50 cm respectively. Determine the length of longest rod which can measure the dimension of the room exactly.
  A)
   75 cm
  done clear
  B)
   70 cm
  done clear
  C)
   69 cm             
  done clear
  D)
   65 cm
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer2)
  Find the smallest number which when increased by 17 is exactly divisible by both 520 and 468.
  A)
   4620               
  done clear
  B)
   4650
  done clear
  C)
   4641                           
  done clear
  D)
   4663
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer3)
  The HCF and LCM of two numbers are 10 and 300 respectively. If one number is 50, then find the other number.
  A)
   60
  done clear
  B)
   15
  done clear
  C)
   45                               
  done clear
  D)
   120
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer4)
  If sum of the squares of zeroes of the polynomial \[f(x)={{x}^{2}}-8x+k\] is 40, then find the value of k.
  A)
   10                               
  done clear
  B)
   11
  done clear
  C)
   12       
  done clear
  D)
   13
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer5)
  When we divide \[(9{{x}^{4}}-4{{x}^{2}}+4)\] by \[(3{{x}^{2}}+x-1),\] then the quotient is:
  A)
   \[2{{x}^{2}}+x\]                   
  done clear
  B)
   \[3{{x}^{2}}-1\]
  done clear
  C)
   \[2x+1\]                      
  done clear
  D)
   \[3{{x}^{2}}-x\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer6)
  If \[\alpha \], \[\beta \] are the roots of \[f(x)={{x}^{2}}-p(x+1)-c,\]then \[(\alpha +1)(\beta +1)\] is equal to:
  A)
  \[c-1\]               
  done clear
  B)
  \[1-c\]
  done clear
  C)
  c                                 
  done clear
  D)
  1+c
  done clear
  E)
  None of these
  done clear
  View Answer play_arrow

• question_answer7)
  Solve: \[\frac{x}{a}+\frac{y}{b}=a+b\] and \[\frac{x}{{{a}^{2}}}+\frac{y}{{{b}^{2}}}=2\]
  A)
   \[x={{a}^{2}}\,and\,\,y={{b}^{2}}\]
  done clear
  B)
   \[x=1\,\,and\,\,y=ab\]
  done clear
  C)
   \[x=a\,\,and\,\,y={{b}^{2}}\] 
  done clear
  D)
   \[x={{a}^{2}}\,\,and\,\,y=b\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer8)
  Find the value of k such that \[kx-y=2\] and \[6x-2y=3\] has unique solution.
  A)
   \[k=2\]                        
  done clear
  B)
   \[k\ne 3\]
  done clear
  C)
   \[k=5\]            
  done clear
  D)
   \[k\ne 4\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer9)
  Ten years ago, father was twelve times as old as his son and ten years hence, lie will be twice as old as his son will be. Find present age of father.
  A)
   20 years                      
  done clear
  B)
   35 years
  done clear
  C)
   39 years                      
  done clear
  D)
   34 years
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer10)
  Find the roots of the equation\[\frac{x}{x-1}+\frac{x+1}{x}=\frac{14}{3},\]\[x\ne 0,\] \[x\ne -\,1\].
  A)
   \[\frac{3}{2}\,\,and\,\,\frac{1}{4}\]
  done clear
  B)
   \[\frac{1}{2}\,\,and\,\,\frac{3}{2}\]
  done clear
  C)
   \[\frac{1}{2}\,\,and\,\,\frac{-\,5}{2}\]                
  done clear
  D)
   \[\frac{-\,3}{2}\,\,and\,\,\frac{5}{2}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer11)
  Sheila can row her boat at a speed of 5 km/h in still water. If it takes 1 hour more to row the boat 5.25 km upstream than to return downstream, then speed of the stream is:
  A)
   \[1\text{ }km/h\]                       
  done clear
  B)
   \[1\,\frac{1}{2}\,\,km/h\]
  done clear
  C)
   \[2\text{ }km/h\]                       
  done clear
  D)
   \[2\,\frac{1}{2}\,\,km/h\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer12)
  A takes 10 days less than the time taken by B to finish a piece of work. If both A and B together can finish the work in 12 days, find the time taken by B alone to finish the work.
  A)
   25 days                       
  done clear
  B)
   27 days
  done clear
  C)
   32 days                       
  done clear
  D)
   30 days
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer13)
  If mth term of an A.P. is \[\frac{1}{n}\] and nth term is \[\frac{1}{m},\] then find its (mn)th term:
  A)
   2                                
  done clear
  B)
   \[-\,1\]
  done clear
  C)
   0                                
  done clear
  D)
   1
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer14)
  What is the sum of three digit natural numbers, which are divisible by 7?
  A)
   70242             
  done clear
  B)
   70639
  done clear
  C)
   70336
  done clear
  D)
   74129
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer15)
  Find the 20th term from the last term of the A.P. 3, 8, 13,...... 253.
  A)
   158     
  done clear
  B)
   162
  done clear
  C)
   154                             
  done clear
  D)
   152
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer16)
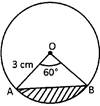
  Find the area of the shaded region from the figure given below.
  A)
   \[0.6125\,\,c{{m}^{2}}\]                     
  done clear
  B)
   \[0.8172\,\,c{{m}^{2}}\]
  done clear
  C)
   \[0.5625\,\,c{{m}^{2}}\]                     
  done clear
  D)
   \[0.4785\,\,c{{m}^{2}}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer17)
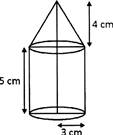
  Find the total surface area of the figure given below.
  A)
   \[141.3\,\,c{{m}^{2}}\]          
  done clear
  B)
   \[145.3\,\,c{{m}^{2}}\]
  done clear
  C)
   \[169.7\,\,c{{m}^{2}}\]          
  done clear
  D)
   \[157.3\,\,c{{m}^{2}}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer18)
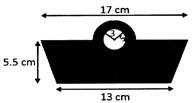
  Find the area of the shaded region in the figure given below (all dimensions are in cm).
  A)
   \[94.7\,\,c{{m}^{2}}\]                        
  done clear
  B)
   \[96.7\,\,c{{m}^{2}}\]
  done clear
  C)
   \[103.7\,\,c{{m}^{2}}\]                      
  done clear
  D)
   \[101.7\,\,c{{m}^{2}}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer19)
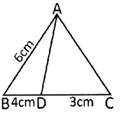
  In the given figure, AD is the bisector of \[\angle A\]. If BD = 4 cm, DC = 3 cm and AB = 6 cm, then find AC.
  A)
   5 cm                           
  done clear
  B)
   3 cm
  done clear
  C)
   4.5 cm            
  done clear
  D)
   3.5 cm
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer20)
  In a \[\Delta \,ABC,\] if D and E are the mid-points of AB and AC respectively, then DE : BC is:
  A)
   2 : 1                            
  done clear
  B)
   1 : 2
  done clear
  C)
   1 : 1                            
  done clear
  D)
   4 : 1
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer21)
  The perimeter of two similar triangles are 25 cm and 15 cm. If one side of first triangle is 9 cm, then find the corresponding side of the other triangle.
  A)
   5.4 cm
  done clear
  B)
   4.2 cm
  done clear
  C)
   5.9 cm            
  done clear
  D)
   6.2 cm
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer22)
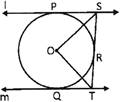
  In the given figure O is the centre of the circle. Find \[\angle SOT,\] if the tangents at the end of the diameter PQ (when joined) are parallel.
  A)
   \[60{}^\circ \] 
  done clear
  B)
   \[90{}^\circ \]
  done clear
  C)
   \[120{}^\circ \]                       
  done clear
  D)
   \[135{}^\circ \]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer23)
  If the angle subtended by two tangents at an outer point is \[60{}^\circ \] and length of the chord formed by joining the point of contact of tangents is 12 cm, then the length of the tangent is given by:
  A)
   4 cm                           
  done clear
  B)
   18 cm
  done clear
  C)
   12 cm
  done clear
  D)
   6 cm
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer24)
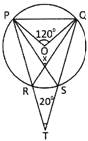
  In the figure given below find the correct value of x, if O is the centre of the circle?
  A)
   \[70{}^\circ \]                         
  done clear
  B)
   \[100{}^\circ \]
  done clear
  C)
   \[120{}^\circ \]           
  done clear
  D)
   \[85{}^\circ \]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer25)
  If \[tan\,A=1\] and \[tan\,B=\sqrt{3},\] find \[\cos \,A\cos \,B\,-\sin \,A\,sin\,B.\]
  A)
   \[\frac{1+\sqrt{3}}{2}\]           
  done clear
  B)
   \[\frac{1-\sqrt{3}}{2\sqrt{2}}\]
  done clear
  C)
   \[\frac{\sqrt{3}}{2\sqrt{2}}\]                 
  done clear
  D)
   \[\frac{2}{\sqrt{3}}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer26)
  If \[\theta \] is an acute angle such that \[{{\tan }^{2}}\theta =\frac{8}{7},\]  then the value of \[\frac{(1+sin\theta )\,\,(1-sin\theta )}{(1+cos\theta )\,\,(1-cos\theta )}\] is:
  A)
   \[\frac{7}{8}\] 
  done clear
  B)
   \[\frac{8}{7}\]
  done clear
  C)
   \[\frac{7}{4}\]                         
  done clear
  D)
   \[\frac{64}{49}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer27)
  If \[\sin \theta +cos\theta =\sqrt{2}\sin \,(90{}^\circ -\theta ),\] then the value of cot 9 is:
  A)
   \[\sqrt{2}+1\]
  done clear
  B)
    \[1-\sqrt{3}\]
  done clear
  C)
   \[2+\sqrt{3}\]              
  done clear
  D)
   \[\sqrt{3+4}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer28)
  Find the coordinates of the mid - point of the line segment joining the points \[A\,\,\left( -\,4,8 \right)\] and \[B\,\,\left( 6,-\,16 \right)\].
  A)
   \[\left( 4,-\,\text{2} \right)\]                     
  done clear
  B)
   \[\left( 1,-\,6 \right)\]
  done clear
  C)
   \[\left( 1,-\,4 \right)\]
  done clear
  D)
   \[\left( -\,3,\text{4} \right)\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer29)
  Find the coordinates of points which trisect the line segment joining the points (1, 3) and (3, 9).
  A)
   \[\left( 5,5 \right)\text{ }and\text{ }\left( 3,3 \right)\]          
  done clear
  B)
   \[\left( 5,5 \right)\text{ }and\text{ }\left( 7,7 \right)\]
  done clear
  C)
   \[\left( \frac{5}{3},\,\,5 \right)\,\,and\,\,\left( \frac{7}{3},\,\,7 \right)\]         
  done clear
  D)
   \[\left( \frac{5}{3},\,\,\frac{7}{3} \right)\,\,and\,\,(5,\,\,7)\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer30)
  If \[P\,\,\left( -\,3,2 \right),\] \[Q\,\,\left( -\,5,-\,5 \right),\] \[R\,\,\left( 2,-\,3 \right)\] and \[S\left( 4,4 \right)\] are the vertices of a quadrilateral, then the quadrilateral will be a:
  A)
   Rectangle                     
  done clear
  B)
   Trapezium
  done clear
  C)
   Rhombus
  done clear
  D)
   Kite
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer31)
  If \[\sum {{f}_{i}}{{x}_{i}}=35,\]\[\sum {{f}_{i}}=4p-63\] and mean=7, then p is equal to:
  A)
   12                               
  done clear
  B)
   13
  done clear
  C)
   14                               
  done clear
  D)
   17
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer32)

  Find x if mode of the following data is 25.
  15	20	25	18	14	15	25	15	18	16	20	25	20	x	18

  A)
   22                               
  done clear
  B)
   25
  done clear
  C)
   27                               
  done clear
  D)
   29
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer33)
  An integer is chosen at random from the number ranging from 1 to 50. The probability that the integer chosen is either a multiple of 2, 3 or 10 is:
  A)
   \[\frac{3}{13}\]                        
  done clear
  B)
   \[\frac{7}{10}\]
  done clear
  C)
   \[\frac{18}{25}\]                                  
  done clear
  D)
   \[\frac{9}{10}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer34)
  A box of 600 bulbs contains 12 defective bulbs. One bulb is taken out at random from the box. Find the probability that it is a non-defective bulb?
  A)
   0.75                            
  done clear
  B)
   0.64
  done clear
  C)
   0.98    
  done clear
  D)
   0.24
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer35)
  There are fifteen horses in a shaddle, of which 5 are black, 2 are red, 6 are white and 2 are of mixed colors. All the black and mixed color horses are hybrid. If one horse is chosen at random, find that it is a hybrid horse.
  A)
   \[\frac{9}{15}\]                        
  done clear
  B)
   \[\frac{1}{5}\]
  done clear
  C)
   \[\frac{7}{15}\]
  done clear
  D)
   \[\frac{1}{3}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer36)
  B is twice as old as A but twice younger than F. C is half the age of A but is twice older than D. Which two persons form the pair of the oldest and the youngest?
  A)
   B and D                      
  done clear
  B)
   F and A
  done clear
  C)
   F and D
  done clear
  D)
   B and F
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer37)
  A walks a distance of 3 km towards north, then turns to his left and walks for 2 km. He again turns left and walks for 3 km. At this point he turns to his right and walks for 3 km. How many km and in what directions is he from the starting point?
  A)
   5 km and west
  done clear
  B)
   3 km and south
  done clear
  C)
   2 km and south
  done clear
  D)
   1 km and east
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer38)
  If the English alphabet A, B, C, ...Z is written in reverse order, then what is the fourth letter to the right of the 12th letter from the left?
  A)
   J                                 
  done clear
  B)
   K
  done clear
  C)
   L                                
  done clear
  D)
   M
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer39)
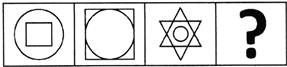
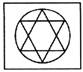
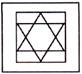
  Find the missing figure having a similar relationship.
  A)
               
  done clear
  B)
   
  done clear
  C)
    
  done clear
  D)
   
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer40)
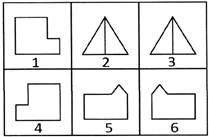
  Group the given figure into three classes using each figure only once.
  A)
   1, 4; 2, 3; 5, 6
  done clear
  B)
   1, 5; 2, 6; 4, 3
  done clear
  C)
   1, 6; 2, 3; 4, 5  
  done clear
  D)
   1, 2; 3, 6; 4, 4
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow