A)
B)
C)
D)
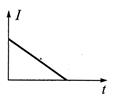
Correct Answer: B
Solution :
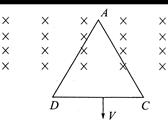
[b] Let la be the side of the triangle and b the length AE. \[\frac{AH}{AE}=\frac{GH}{EC}\] \[\therefore \,\,\,\,\,GH=\frac{AH}{AE}.EC\] \[\therefore \,\,\,\,\,FG=2GH=2\left[ a-\frac{a}{b}vt \right]\] Induced EMF, \[eBv(FG)=2Bv\left( a-\frac{a}{b}tv \right)\]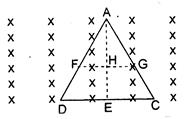 Induced current, \[I=\frac{e}{R}=\frac{2Bv}{R}\left[ a-\frac{a}{b}tv \right]\] or \[l={{k}_{1}}-{{k}_{2}}t\] Thus, \[I-t\]graph is a straight line with negative slope and positive intercept.
Induced current, \[I=\frac{e}{R}=\frac{2Bv}{R}\left[ a-\frac{a}{b}tv \right]\] or \[l={{k}_{1}}-{{k}_{2}}t\] Thus, \[I-t\]graph is a straight line with negative slope and positive intercept.
You need to login to perform this action.
You will be redirected in
3 sec
