question_answer

A particle is projected under gravity with velocity \[\sqrt{2ag}\] from a point at a height h above the level plane at an angle \[\theta \] to it. The maximum range R on the ground is          

A) \[\sqrt{\left( {{a}^{2}}+1 \right)h}\]           

B)        \[\sqrt{{{a}^{2}}h}\]               

C) \[\sqrt{ah}\]               

D)        \[2\sqrt{a(a+h)}\]

Correct Answer: D

Solution :

[d] Coordinates of point P are \[(R,-h)\].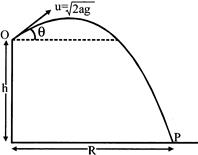 Hence \[-h=R\tan \theta -\frac{g{{R}^{2}}}{2\left( 2ga \right)}\left( 1+{{\tan }^{2}}\theta  \right)\] \[\Rightarrow \,\,\,\,{{R}^{2}}{{\tan }^{2}}\theta -4aR\,\,\tan \theta +({{R}^{2}}-4ah)=0\] For \[\theta \] to be real, \[{{(4aR)}^{2}}\ge 4{{R}^{2}}({{R}^{2}}-4ah)\] \[\Rightarrow \,\,\,4{{a}^{2}}\ge ({{R}^{2}}-4ah)\Rightarrow {{R}^{2}}\le 4a(a+h)\] \[\Rightarrow \,\,R\le 2\sqrt{a(a+h)}\,\,\,\,\,\Rightarrow \,\,\,\,\,\,{{R}_{\max }}=2\sqrt{a(a+h)}\]