A) \[\frac{m}{(m+M)}v\]
B) \[\frac{m}{2M}v\]
C) \[\frac{2m}{M}v\]
D) \[\frac{(m+M)}{2m}v\]
Correct Answer: B
Solution :
[b] The rope tension is the same both on the left and right hand side at every instant, and consequently momentum of both sides are equal. \[\therefore \,\,\,Mv=(M+m)(-v)+m({{v}_{r}}-v)\]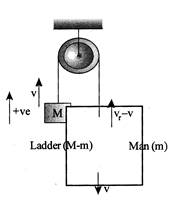 Or \[v=\frac{m}{2M}{{v}_{F}}\] Momentum of the centre of mass is \[P={{P}_{1}}+{{P}_{2}}\] Or \[2M{{v}_{com}}=Mv+Mv\] \[\therefore \,\,\,\,{{v}_{com}}=v=\frac{m}{2M}{{v}_{r}}\]
Or \[v=\frac{m}{2M}{{v}_{F}}\] Momentum of the centre of mass is \[P={{P}_{1}}+{{P}_{2}}\] Or \[2M{{v}_{com}}=Mv+Mv\] \[\therefore \,\,\,\,{{v}_{com}}=v=\frac{m}{2M}{{v}_{r}}\]
You need to login to perform this action.
You will be redirected in
3 sec
