question_answer

Two particles A and B, each of mass m and moving with velocity v, hit the ends of a rigid bar of mass M and length simultaneously and stick to the bar. The bar is kept on a smooth horizontal plane (as shown). Find the angular speed of the system (bar + particle) after the collision. \[[M=6m]\]           

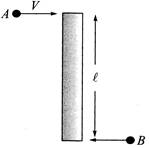
A) \[\frac{2v}{\ell }\]                             

B)        \[\frac{v}{\ell }\]                 

C) \[\frac{3v}{\ell }\]                     

D)        zero

Correct Answer: B

Solution :

  [b] Conservation of linear momentum \[{{P}_{i}}=mv-mv=0\] \[\Rightarrow \,\,\,\,\,\,\,\,\,{{V}_{cm}}=0\] Conservation of angular momentum \[\Rightarrow \,\,\,\,\,\,{{L}_{initial}}={{L}_{final}}\] where \[{{L}_{initial}}=\left| \frac{m\ell }{2}v+\frac{m\ell }{2}v \right|=mv\ell \]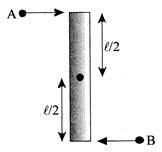 Let the system rotate about its cm 'O' with an angular speed \[\omega \]. \[\Rightarrow \,\,\,\,\,\,\,\,{{L}_{final}}=\left( {{I}_{system}} \right)\omega \] where \[{{I}_{system}}=\frac{M{{\ell }^{2}}}{12}+m{{\left( \frac{\ell }{2} \right)}^{2}}+m{{\left( \frac{\ell }{2} \right)}^{2}}=\left( \frac{M+6m}{12} \right){{\ell }^{2}}\] \[\therefore \,\,\,\,\,\,\,\left( \frac{M+6m}{12} \right)\omega {{\ell }^{2}}=nv\ell \] \[\Rightarrow \,\,\,\,\,\,\,\,\omega =\frac{12mv}{(M+6m)\ell }\].