question_answer

The greatest integral value of a such that \[\sqrt{9-{{a}^{2}}+2x-{{x}^{2}}}\ge \sqrt{16-{{x}^{2}}}\] for at least one positive value of x is

A) \[3\]                      

B)        \[4\]                      

C) \[6\]                      

D)        \[7\]

Correct Answer: D

Solution :

[d] We have \[y=\sqrt{9-{{a}^{2}}+2ax-{{x}^{2}}}\] \[\Rightarrow \,\,\,\,\,\,{{y}^{2}}+{{(x-a)}^{2}}=9\] And    \[y=\sqrt{16-{{x}^{2}}}\]           \[\Rightarrow \,\,\,\,\,\,\,{{y}^{2}}+{{x}^{2}}=16\] The given equations represent semicircles.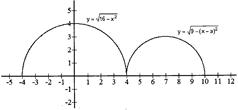 If  \[a>7,\] then no solution exists. Thus, \[a\le 7\].\ Hence, maximum value of a is 7.