2. Sample Papers
  3. JEE Main & Advanced

JEE Main & Advanced Sample Paper JEE Main Sample Paper-19

  • question_answer
    Two masses A and B of \[10\text{ }kg\] and \[5\text{ }kg\] respectively are connected with a string passing over a frictionless pulley fixed at the corner of a table (as shown in figure). The coefficient of friction between the table and the block is\[0.2\]. The minimum mass of C that may be placed on A to prevent it from moving is equal to            

    A)  \[15\text{ }kg\]                         

    B)  \[10\text{ }kg\]

    C)  \[5\,kg\]                       

    D)  \[0\,kg\]

    Correct Answer: A

    Solution :

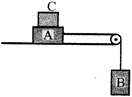
     Let T be the tension in the string; f= frictional force between block A and table; m?= minimum mass of C. For the just motion of block A on table \[T=f=\mu R=\mu (m+m')g=0.2(10+m')g\] ?.(i) For the just motion of block B, \[T=\text{ }5g\]  ....(ii) From (i) and (ii), \[5g=0.2(10+m')g\] or \[5=2+0.2m'\] or \[m'=\frac{5-2}{0.2}=15kg\]


You need to login to perform this action.
You will be redirected in 3 sec spinner