question_answer

Two long parallel wires P and Q are both perpendicular to    the plane of the paper with distance of 5 m between them. If            P and Q carry current of \[2.5\] amp and 5 amp respectively in the same direction, then the magnetic field at a point half-way between the wires is       

A)  \[\frac{3{{\mu }_{0}}}{2\pi }\]                 

B)  \[\frac{{{\mu }_{0}}}{\pi }\]

C)  \[\frac{\sqrt{3}{{\mu }_{0}}}{2\pi }\]                     

D)  \[\frac{{{\mu }_{0}}}{2\pi }\]

Correct Answer: A

Solution :

 When current flow in both wire in same direction then magnetic field at halfway due to P wire. \[{{\overrightarrow{B}}_{P}}=\frac{{{\mu }_{0}}{{I}_{1}}}{2\pi \frac{5}{2}}=\frac{{{\mu }_{0}}{{I}_{1}}}{\pi .5}=\frac{{{\mu }_{0}}}{\pi }\] (Where \[{{I}_{1}}=5\,A\]Amp) The direction of \[{{B}_{P}}\] is downward \[\odot \]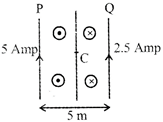                 Magnetic field at halfway due to Q wire \[{{\overrightarrow{B}}_{Q}}=\frac{{{\mu }_{0}}{{I}_{2}}}{2\pi \frac{5}{2}}=\frac{{{\mu }_{0}}}{2\pi }\] [upward \[\otimes \]] [Where \[{{I}_{2}}=2.5\] Amp.] Net magnetic field at halfway \[\overrightarrow{B}={{\overrightarrow{B}}_{P}}+{{\overrightarrow{B}}_{Q}}=\frac{{{\mu }_{0}}}{\pi }+\frac{{{\mu }_{0}}}{2\pi }=\frac{3{{\mu }_{0}}}{2\pi }\] (downward\[\odot \]) Hence net magnetic field at midpoint \[=\frac{3{{\mu }_{0}}}{2\pi }\]