question_answer

In a circuit L, C and R are connected in series with an alternating voltage source of frequency f The current leads the voltage by \[{{45}^{o}}\]. The value of C is          

A)  \[\frac{1}{\pi (2\pi fL-R)}\]                           

B)  \[\frac{1}{2\pi (2\pi fL-R)}\]

C)  \[\frac{1}{\pi f(2\pi fL+R)}\]      

D)  \[\frac{1}{2\pi f(2\pi fL+R)}\]

Correct Answer: D

Solution :

 From figure,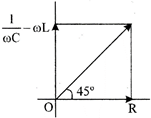 \[\tan {{45}^{o}}=\frac{\frac{1}{\omega C}-\omega L}{R}\] \[\Rightarrow \] \[\frac{1}{\omega C}-\omega L=R\Rightarrow \frac{1}{\omega C}=R+\omega L\] \[C=\frac{1}{\omega (R+\omega )}=\frac{1}{2\pi f\,(R+2\pi fL)}\]