A) \[\frac{9}{4\pi }c{{m}^{3}}/\min \]
B) \[\frac{1}{4\pi }c{{m}^{3}}/\min \]
C) \[\frac{1}{9\pi }c{{m}^{3}}/\min \]
D) \[\frac{4}{9\pi }c{{m}^{3}}/\min \]
Correct Answer: D
Solution :
Let \[y\] be the level of water at time \[t\] and \[x\] the radius of the surface and \[V\], the volume of water. We know that the volume of cone \[=\frac{1}{3}\pi {{(radius)}^{2}}\times height\]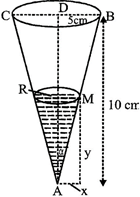 \[\therefore \] \[V=\frac{1}{3}\pi {{x}^{2}}y.\] Let\[\angle BAD=\alpha \] \[\Rightarrow \] \[\tan \alpha =\frac{BD}{AD}=\frac{5}{10}=\frac{1}{2}\] Again, from right angled \[\Delta AMR\], we have \[\tan \alpha =\frac{MR}{AR}=\frac{x}{y};\,\,\Rightarrow \frac{1}{2}=\frac{x}{y};\,\,\,\,x=\frac{y}{2}\]. \[\therefore \]\[V=\frac{1}{3}\pi {{x}^{2}}y=\frac{1}{3}\pi {{\left( \frac{y}{2} \right)}^{2}}\cdot y=\frac{\pi }{12}{{y}^{2}}\] ? (1) By question, the rate of change of volume \[=\frac{dV}{dt}=4\,\,cub.cm/\min \] We have to find out the rate of increase of water-level\[i.e.,\]\[\frac{dy}{dt}.\] Differentiating (1) with respect to\[t\], we get \[\frac{dV}{dt}=\frac{\pi }{12}.3{{y}^{2}}\cdot \frac{dy}{dt};\,\,\therefore 4=\frac{\pi }{4}{{y}^{2}}\cdot \frac{dy}{dt};\,\,\therefore \frac{dy}{dt}=\frac{16}{\pi {{y}^{2}}}\]When\[y=6\,\,cm,\,\,\frac{dy}{dt}=\frac{16}{\pi {{6}^{2}}}=\frac{4}{9\pi }cub.cm/\min \]
\[\therefore \] \[V=\frac{1}{3}\pi {{x}^{2}}y.\] Let\[\angle BAD=\alpha \] \[\Rightarrow \] \[\tan \alpha =\frac{BD}{AD}=\frac{5}{10}=\frac{1}{2}\] Again, from right angled \[\Delta AMR\], we have \[\tan \alpha =\frac{MR}{AR}=\frac{x}{y};\,\,\Rightarrow \frac{1}{2}=\frac{x}{y};\,\,\,\,x=\frac{y}{2}\]. \[\therefore \]\[V=\frac{1}{3}\pi {{x}^{2}}y=\frac{1}{3}\pi {{\left( \frac{y}{2} \right)}^{2}}\cdot y=\frac{\pi }{12}{{y}^{2}}\] ? (1) By question, the rate of change of volume \[=\frac{dV}{dt}=4\,\,cub.cm/\min \] We have to find out the rate of increase of water-level\[i.e.,\]\[\frac{dy}{dt}.\] Differentiating (1) with respect to\[t\], we get \[\frac{dV}{dt}=\frac{\pi }{12}.3{{y}^{2}}\cdot \frac{dy}{dt};\,\,\therefore 4=\frac{\pi }{4}{{y}^{2}}\cdot \frac{dy}{dt};\,\,\therefore \frac{dy}{dt}=\frac{16}{\pi {{y}^{2}}}\]When\[y=6\,\,cm,\,\,\frac{dy}{dt}=\frac{16}{\pi {{6}^{2}}}=\frac{4}{9\pi }cub.cm/\min \]
You need to login to perform this action.
You will be redirected in
3 sec
