A) 1
B) 2
C) 1
D) 4
Correct Answer: B
Solution :
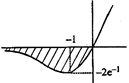 Let \[f(x)=y\] \[\Rightarrow \,\,\frac{dy}{dx}-y=2{{e}^{x}};\] Integrating factor \[={{e}^{-x}}\] \[\therefore \,\,y.{{e}^{-x}}=\int_{{}}^{{}}{2{{e}^{x}}{{e}^{-x}}\,dx=2x+C}\] Now, \[y(0)=0\Rightarrow \,C=0\] \[\Rightarrow \,f(x)\,=y=2x{{e}^{x}}\] \[\therefore \,\,\frac{dy}{dx}\,=2[x{{e}^{x}}+{{e}^{x}}]\,=0\] \[\Rightarrow \,x=-1\] \[A=2\int\limits_{-\infty }^{0}{x{{e}^{x}}dx=2\left[ x{{e}^{x}}-\int\limits_{-\infty }^{0}{{{e}^{x}}dx} \right]}\] \[=2\left[ x{{e}^{x}}-{{e}^{x}} \right]_{-\infty }^{0}=2\,(-1)\,-(0-0)\,]\,=-2\] Hence area is 2.
Let \[f(x)=y\] \[\Rightarrow \,\,\frac{dy}{dx}-y=2{{e}^{x}};\] Integrating factor \[={{e}^{-x}}\] \[\therefore \,\,y.{{e}^{-x}}=\int_{{}}^{{}}{2{{e}^{x}}{{e}^{-x}}\,dx=2x+C}\] Now, \[y(0)=0\Rightarrow \,C=0\] \[\Rightarrow \,f(x)\,=y=2x{{e}^{x}}\] \[\therefore \,\,\frac{dy}{dx}\,=2[x{{e}^{x}}+{{e}^{x}}]\,=0\] \[\Rightarrow \,x=-1\] \[A=2\int\limits_{-\infty }^{0}{x{{e}^{x}}dx=2\left[ x{{e}^{x}}-\int\limits_{-\infty }^{0}{{{e}^{x}}dx} \right]}\] \[=2\left[ x{{e}^{x}}-{{e}^{x}} \right]_{-\infty }^{0}=2\,(-1)\,-(0-0)\,]\,=-2\] Hence area is 2.
You need to login to perform this action.
You will be redirected in
3 sec
