question_answer

Consider two lines in space as \[{{L}_{i}}={{\vec{r}}_{1}}=\hat{j}+2\hat{k}+\lambda (3\hat{i}-\hat{j}-\hat{k})\] And          \[{{L}_{2}}={{\vec{r}}_{2}}=4\hat{i}+3\hat{j}+6\hat{k}+\mu (\hat{i}+2\hat{k})\]. If the shortest distance between these lines is \[\sqrt{d}\] then d equals

A)  5                                

B)  6

C)  7                                

D)  8

Correct Answer: B

Solution :

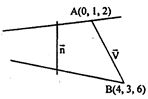Vector perpendicular to both \[\vec{n}=\left| \begin{matrix}    {\hat{i}} & {\hat{j}} & {\hat{k}}  \\    3 & -1 & -1  \\    1 & 0 & 2  \\ \end{matrix} \right|\] \[=\hat{i}(-2)\,-\hat{j}(6+1)\,+\hat{k}(0+1)\] \[=-2\hat{i}-7\hat{j}+\hat{k}\] says \[2\hat{i}+7\hat{j}-\hat{k}\] Now \[\vec{V}=\overrightarrow{AB}=4\hat{i}+2\hat{j}+4\hat{k}\] Now \[S.D.\,=\left| \frac{V.n}{|n|} \right|\,=\left| \frac{18+14-4}{\sqrt{54}} \right|\,=\frac{18}{\sqrt{54}}\,=\frac{18}{3\sqrt{6}}\,=\frac{6}{\sqrt{6}}\] \[\therefore \,\,S.D=\sqrt{6}\Rightarrow \,d=6\]