A) straight line
B) circle
C) parabola
D) hyperbola
Correct Answer: B
Solution :
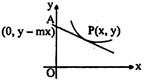 \[Y-y\,=m(X-x)\] Put \[X=0\] \[Y=y-mx\] Hence \[A\equiv \,(0,\,\,y-mx)\] \[\therefore \,\,OA=OP\] \[\Rightarrow \,\,|y-mx{{|}^{2}}={{x}^{2}}+{{m}^{2}}{{x}^{2}}\] \[\Rightarrow \,\,{{y}^{2}}+{{m}^{2}}{{x}^{2}}-2xym\,={{x}^{2}}\,+{{m}^{2}}{{x}^{2}}\] \[\therefore \,\frac{dy}{dx}\,=\frac{{{y}^{2}}-{{x}^{2}}}{2xy}\,\Rightarrow \,\,2xy\,\frac{dy}{dx}\,={{y}^{2}}-{{x}^{2}}\] Now put \[{{y}^{2}}=t\Rightarrow \,2y\,\frac{dy}{dx}\,=\frac{dt}{dx}\] \[\therefore \,\,x\frac{dt}{dx}=t-{{x}^{2}};\,\,\frac{dt}{dx}-\frac{1}{x}\,t=-x\] Integrating factor \[={{e}^{-\frac{1}{x}dx}}\,={{e}^{-\ln x}}=\frac{1}{x};\] Hence \[\frac{1}{x}.t=-\int_{{}}^{{}}{dx;\,\frac{t}{x}\,=-x+C}\] \[\therefore \,\,{{y}^{2}}=-{{x}^{2}}+Cx & ;\] \[\Rightarrow \,{{x}^{2}}+{{y}^{2}}\,=Cx\Rightarrow \,\] Circle.
\[Y-y\,=m(X-x)\] Put \[X=0\] \[Y=y-mx\] Hence \[A\equiv \,(0,\,\,y-mx)\] \[\therefore \,\,OA=OP\] \[\Rightarrow \,\,|y-mx{{|}^{2}}={{x}^{2}}+{{m}^{2}}{{x}^{2}}\] \[\Rightarrow \,\,{{y}^{2}}+{{m}^{2}}{{x}^{2}}-2xym\,={{x}^{2}}\,+{{m}^{2}}{{x}^{2}}\] \[\therefore \,\frac{dy}{dx}\,=\frac{{{y}^{2}}-{{x}^{2}}}{2xy}\,\Rightarrow \,\,2xy\,\frac{dy}{dx}\,={{y}^{2}}-{{x}^{2}}\] Now put \[{{y}^{2}}=t\Rightarrow \,2y\,\frac{dy}{dx}\,=\frac{dt}{dx}\] \[\therefore \,\,x\frac{dt}{dx}=t-{{x}^{2}};\,\,\frac{dt}{dx}-\frac{1}{x}\,t=-x\] Integrating factor \[={{e}^{-\frac{1}{x}dx}}\,={{e}^{-\ln x}}=\frac{1}{x};\] Hence \[\frac{1}{x}.t=-\int_{{}}^{{}}{dx;\,\frac{t}{x}\,=-x+C}\] \[\therefore \,\,{{y}^{2}}=-{{x}^{2}}+Cx & ;\] \[\Rightarrow \,{{x}^{2}}+{{y}^{2}}\,=Cx\Rightarrow \,\] Circle.
You need to login to perform this action.
You will be redirected in
3 sec
