question_answer

If the area bounded by the graph of \[y=x\,{{e}^{-ax}}(a>0)\] and the abscissa axis is \[\frac{1}{9}\] then the value of 'a' is equal to

A)  1                    

B)  4

C)  6                                

D)  9

Correct Answer: A

Solution :

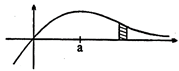\[y=x{{e}^{-ax}}\] \[\Rightarrow \,{{y}^{t}}={{e}^{-ax}}-xa{{e}^{-ax}}\] \[={{e}^{-ax}}(1-ax)=0\] \[\therefore \,x=\frac{1}{a}\] as \[x\to \infty ,\,y\to 0\] \[x\to -\infty ,\,y\to \infty \] \[A=\left. \int\limits_{a}^{\infty }{\underbrace{x}_{{}}\underbrace{{{e}^{-ax}}}_{{}}dx\,=\frac{x.{{e}^{-ax}}}{-a}} \right]_{a}^{\infty }\] \[\left. +\frac{1}{a}\,\int_{0}^{\infty }{{{e}^{-ax}}dx=(0)\,-\frac{1}{{{a}^{2}}}{{e}^{-ax}}\,} \right]_{0}^{\infty }\,=\frac{-1}{{{a}^{2}}}[0-1]\,=\frac{1}{{{a}^{2}}}\] \[\therefore \,\,\frac{1}{{{a}^{2}}}\,=\frac{1}{9}\Rightarrow \,\,a=3\]