question_answer

Let a circle of radius \[\frac{2}{\sqrt{3}}\] is touching the lines \[{{x}^{2}}-4xy+{{y}^{2}}=0\]in the first quadrant at points A and B. If area of triangle OAB (0 being the origin) is \[\Delta \] then \[{{\Delta }^{2}}\] equals

A)  1                    

B)  3

C)  2                                

D)  1

Correct Answer: B

Solution :

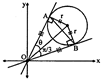Here \[\tan 2\theta \,=\frac{2\sqrt{4}-1}{2}\,=\sqrt{3}\,\Rightarrow \,\theta \,=\frac{\pi }{6}\] \[\therefore \,\,\] Area of \[\Delta OAB=\frac{1}{2}{{(r\cos \theta )}^{2}}(\sin 2\theta )\] \[=\frac{1}{2}\,{{\left( r\sqrt{3} \right)}^{2}}\frac{\sqrt{3}}{2}\,=\frac{3\sqrt{3}{{r}^{2}}}{4}\] \[={{\Delta }^{2}}=3\,\,\left( As\,r=\frac{2}{\sqrt{3}} \right)\]