2. Sample Papers
  3. JEE Main & Advanced

JEE Main & Advanced Sample Paper JEE Main Sample Paper-32

  • question_answer
    The orbital velocity of a satellite at point B with radius \[{{r}_{B}}\] is v. The radius of point A is \[{{r}_{A}}.{{r}_{A}}\]and \[{{r}_{B}}\] are semi major and semi minor axis respectively. If the orbit is increased in radial direction so that \[{{r}_{A}}\] becomes 1\[1.2{{r}_{A}}\]. find the orbital velocity at \[(1.2{{r}_{A}})\]

    A) \[\frac{v{{r}_{B}}}{{{r}_{A}}\sqrt{1.2}}\]

    B)    \[\frac{v{{r}_{A}}}{1.2{{r}_{B}}}\]

    C) \[\frac{v{{r}_{B}}}{1.2{{r}_{A}}}\]                             

    D) \[\frac{v{{r}_{B}}}{{{r}_{B}}\sqrt{1.2}}\]

    Correct Answer: A

    Solution :

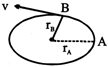
    For two points on same orbit                 \[L=m{{v}_{A}}{{r}_{A}}=mv{{r}_{B}}\]                 \[{{v}_{A}}=\frac{v{{r}_{B}}}{{{r}_{A}}}\]                 For two points on different orbits. \[v=\sqrt{\frac{GM}{r}}\] \[\frac{{{v}_{0}}}{{{v}_{A}}}={{\left( \frac{{{r}_{A}}}{1.2{{r}_{A}}} \right)}^{1/2}}\] \[{{v}_{0}}={{v}_{A}}{{\left( \frac{{{r}_{A}}}{1.2{{r}_{A}}} \right)}^{1/2}}\] \[=\frac{v{{r}_{B}}}{{{r}_{A}}\sqrt{1.2}}\]


You need to login to perform this action.
You will be redirected in 3 sec spinner