Hence, rate at the start of the reaction is
A) \[1.25\text{ }mol\text{ }{{L}^{-1}}\text{ }mi{{n}^{-1}}\]
B) \[0.125\text{ }mol\text{ }{{L}^{-1\text{ }}}mi{{n}^{-1}}\]
C) \[0.5\text{ }mol\text{ }{{L}^{-1}}\text{ }mi{{n}^{-1}}\]
D) \[1.25\text{ }mol\text{ }mi{{n}^{-1}}\]
Correct Answer: B
Solution :
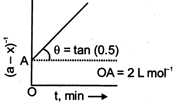
Since the graph of \[t\,\,vs\,{{(a-x)}^{-1}}\] is a straight line it must be a second order reaction. \[\therefore \,\,K=\frac{1}{t}\,\left[ \frac{1}{(a-x)}-\frac{1}{a} \right]\] Or \[\,\frac{1}{(a-x)}\,=Kt+\frac{1}{a}\] On comparing, slope \[K=\tan \theta \,=0.5\,mo{{l}^{-1}}\,L\,{{\min }^{-1}}\] \[OA=\frac{1}{a}\,=2L\,mo{{l}^{-1}}\] Or \[a=0.5\,mol\,{{L}^{-1}}\] \[Rate\,=K{{(a)}^{2}}=0.5\,\times {{(0.5)}^{2}}\] \[=0.125\,mol\,{{L}^{-1}}\,\]
You need to login to perform this action.
You will be redirected in
3 sec
