question_answer

The minimum value of \[|{{z}_{1}}-{{z}_{2}}|\] as \[{{z}_{1}}\] and \[{{z}_{2}}\] vary over the curve  \[|\sqrt{3}(1-2z)+2i|=2\sqrt{7}\]and \[|\sqrt{3}(-1-z)-2i|=\sqrt{3}(9-z)+18i|\] respectively, is [Note: \[i=\sqrt{-1}\]]

A)  \[\frac{7\sqrt{7}}{2\sqrt{3}}\]                  

B)  \[\frac{5\sqrt{7}}{2\sqrt{3}}\]

C)  \[\frac{14\sqrt{7}}{\sqrt{3}}\]                  

D)  \[\frac{7\sqrt{7}}{5\sqrt{3}}\]

Correct Answer: B

Solution :

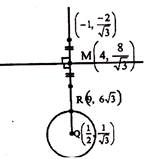\[|\,\sqrt{3}\,(1-2z)+2i\,|\,=2\sqrt{7}\] is the equation of circle having centre is \[\left( \frac{1}{2},\frac{1}{\sqrt{3}} \right)\] and having radius\[\frac{\sqrt{7}}{3}\]. Also, \[\left| \,\sqrt{3}(1-2z)-2i \right|=\left| \sqrt{3}(9-z)+18i \right|\] Is the equation of perpendicular bisector of line joining \[\left( -1,\frac{-2}{\sqrt{3}} \right)\] and \[\left( 9,6\sqrt{3} \right)\] So, \[MQ=\sqrt{{{\left( 4-\frac{1}{2} \right)}^{2}}+{{\left( \frac{8}{\sqrt{3}}-\frac{1}{\sqrt{3}} \right)}^{2}}}=\frac{7\sqrt{7}}{2\sqrt{3}}\] \[\therefore \]Required distance \[=(MQ)-\] (radius) \[=\frac{7\sqrt{7}}{2\sqrt{3}}-\sqrt{\frac{7}{3}}=\frac{5}{2}\sqrt{\frac{7}{3}}\]