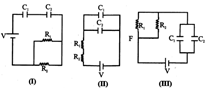
A) \[18,\frac{8}{9},4\]
B) \[18,4\frac{8}{9}\]
C) \[4,\frac{8}{9},18\]
D) \[\frac{8}{9},18,4\]
Correct Answer: D
Solution :
since \[\tau =RC\] where R is effective resistance across the effective capacitor while the battery or batteries are shortcircuited and C is effective capacitance. In 1, \[R=\frac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}=\frac{2}{3}\Omega \] and \[C=\frac{{{C}_{1}}{{C}_{2}}}{{{C}_{1}}+{{C}_{2}}}=\frac{4}{3}\,\mu F\] \[\therefore \,\,\tau \,\,=RC\,=\frac{8}{9}\,\mu s\] In II, \[R={{R}_{1}}+{{R}_{2}}=3\Omega \] and \[C={{C}_{1}}+{{C}_{2}}\,=6\mu F\] \[\therefore \,\,\tau \,=RC=18\,\mu s\] \[R=\frac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}\,=\frac{2}{3}\,\Omega \] and \[C={{C}_{1}}+{{C}_{2}}=6\mu F\] \[\therefore \,\,\tau =RC\,=4\mu s\]You need to login to perform this action.
You will be redirected in
3 sec
