question_answer

A cylinder of radius R made of a material of thermal conductivity \[{{K}_{1}}\] is surrounded by a cylindrical shell of inner radius R & outer radius 2R made of a material of thermal conductivity \[{{K}_{2}}.\]The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. The effective thermal conductivity of the system is

A)  \[{{K}_{1}}+{{K}_{2}}\]                 

B) \[{{K}_{1}}{{K}_{2}}/({{K}_{1}}+{{K}_{2}})\]

C) \[({{K}_{1}}+3{{K}_{2}})/4\]                        

D)  \[(3{{K}_{1}}+{{K}_{2}})/4\]

Correct Answer: C

Solution :

 Heat flowing per sec. through cylinder of radius R, \[{{Q}_{1}}={{K}_{1}}(\pi {{R}^{2}})\left( \frac{{{T}_{1}}-{{T}_{2}}}{l} \right)\] Heat flowing per sec through outer shell of radius 2R, \[{{Q}_{2}}={{K}_{2}}(\pi {{(2R)}^{2}}-\pi {{R}^{2}})\left( \frac{{{T}_{1}}-{{T}_{2}}}{l} \right)\] Total\[Q={{Q}_{1}}+{{Q}_{2}}=({{K}_{1}}+3{{K}_{2}})\pi {{R}^{2}}\left( \frac{{{T}_{1}}-{{T}_{2}}}{l} \right)\]?(1)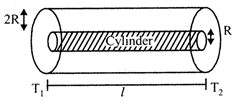 Let K be the equivalent thermal conductivity  of the system. Then \[Q=K\pi {{(2R)}^{2}}\left( \frac{{{T}_{1}}-{{T}_{2}}}{l} \right)\]                      ....(2) From eqs. (1) and (2), we have \[({{K}_{1}}+3{{K}_{2}})=4K\]or\[K=\frac{{{K}_{1}}+3{{K}_{2}}}{4}\]