question_answer

Area included between \[y=\frac{{{x}^{2}}}{4a}\]and \[y=\frac{8{{a}^{3}}}{{{x}^{2}}+4{{a}^{2}}}\]is

A)  \[\frac{{{a}^{2}}}{3}(6\pi -4)\]                  

B)  \[\frac{{{a}^{2}}}{3}(4\pi +3)\]

C)  \[\frac{{{a}^{2}}}{3}(8\pi +3)\]                 

D)  none of these

Correct Answer: A

Solution :

 The curve of y (x2 + 4a2) = 8a3 is symmetrical about y-axis and cuts it at A (0,2a). Tangent at A is parallel to x-axis. x-axis is asymptote. This curve meets x2 = 4ay Where, \[\frac{{{x}^{2}}}{4a}=\frac{8{{a}^{3}}}{{{x}^{2}}+4{{a}^{2}}}\Rightarrow {{x}^{4}}+4{{a}^{2}}{{x}^{2}}-32{{a}^{4}}=0\] \[\Rightarrow \]\[({{x}^{2}}-4{{a}^{2}})({{x}^{2}}+8{{a}^{2}})=0\Rightarrow x=\pm 2a\] \[\therefore \]Required area \[=2\left[ \int_{0}^{2a}{\frac{8{{a}^{3}}}{{{x}^{2}}+4{{a}^{2}}}dx-\int_{0}^{2a}{\frac{{{x}^{2}}}{4a}}dx} \right]\]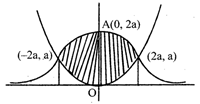 \[=\frac{{{a}^{2}}}{3}(6\pi -4).\]