A) \[2\,m{{v}^{2}}\]
B) \[\frac{3}{2}\,m{{v}^{2}}\]
C) \[\frac{1}{2}\,m{{v}^{2}}\]
D) \[3\,m{{v}^{2}}\]
Correct Answer: B
Solution :
The resultant momentum of two particles which fly-off at right angles is \[\Rightarrow \]. By law of conservation of momentum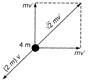 \[\Rightarrow \] \[|{{M}^{-1}}|\,|adj\,(adjM)|\,=\,|kI|\] \[=100\,\left( \frac{\Delta \phi }{\Delta t} \right)\] Total energy released E is the sum of kinetic energies of all the three particles \[=5\times {{10}^{-3}}\times 100=0.5\,\,V\] \[R=v\sqrt{\frac{2h}{g}}\] \[u=v,\] \[u=v+at\]
\[\Rightarrow \] \[|{{M}^{-1}}|\,|adj\,(adjM)|\,=\,|kI|\] \[=100\,\left( \frac{\Delta \phi }{\Delta t} \right)\] Total energy released E is the sum of kinetic energies of all the three particles \[=5\times {{10}^{-3}}\times 100=0.5\,\,V\] \[R=v\sqrt{\frac{2h}{g}}\] \[u=v,\] \[u=v+at\]
You need to login to perform this action.
You will be redirected in
3 sec
