A) \[{{\lambda }_{1}}+{{\lambda }_{2}}\]
B) \[\frac{2{{\lambda }_{1}}{{\lambda }_{2}}}{\sqrt{\lambda _{1}^{2}+\lambda _{2}^{2}}}\]
C) \[\frac{{{\lambda }_{1}}{{\lambda }_{2}}}{\sqrt{|\lambda _{1}^{2}+\lambda _{2}^{2}|}}\]
D) \[\frac{{{\lambda }_{1}}+{{\lambda }_{2}}}{2}\]
Correct Answer: B
Solution :
Let, m is the mass of each particle, then \[SD=\sqrt{{{60}^{2}}+{{25}^{2}}}\] at \[=\sqrt{4225}=65=DP\], where \[\Delta x=(SA+AP)-SP\] and \[\Rightarrow \] are the velocities of two particles as shown in figure.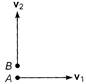 \[\Delta x=(65+65)-120\] Velocity of A w.r.t. C frame is \[\Rightarrow \] \[\Delta x=10\,m\] (as angle between \[\frac{\lambda }{2}\] and \[\lambda \] is \[=\left( 10-\frac{\lambda }{2} \right)\]) So, required wavelength is \[=(2n)\frac{\lambda }{2}\] (as \[n=0,\,\,1,\,\,2,...\]) \[10-\frac{\lambda }{2}=(2n)\frac{\lambda }{2},\,\,n=0,\,\,1,\,2,...\] \[10=(2n+1)\frac{\lambda }{2},\,n=0,\,1,\,\,2,...\]
\[\Delta x=(65+65)-120\] Velocity of A w.r.t. C frame is \[\Rightarrow \] \[\Delta x=10\,m\] (as angle between \[\frac{\lambda }{2}\] and \[\lambda \] is \[=\left( 10-\frac{\lambda }{2} \right)\]) So, required wavelength is \[=(2n)\frac{\lambda }{2}\] (as \[n=0,\,\,1,\,\,2,...\]) \[10-\frac{\lambda }{2}=(2n)\frac{\lambda }{2},\,\,n=0,\,\,1,\,2,...\] \[10=(2n+1)\frac{\lambda }{2},\,n=0,\,1,\,\,2,...\]
You need to login to perform this action.
You will be redirected in
3 sec
