A) The force exerted by light on the sphere is the greatest when surface of sphere is perfectly reflecting and is equal to \[\frac{2l\times \pi {{R}^{2}}}{c}\]
B) The force exerted by light on the sphere is independent of the nature of surface, i.e.. it is same for perfect reflector, perfect absorber, and is partially reflecting and for all it is equal to \[\frac{l\times \pi {{R}^{2}}}{c}\].
C) The force exerted by light on sphere is least when surface of the sphere a is perfect absorber, and is equal to \[\frac{l\times \pi {{R}^{2}}}{c}\].
D) Both [a] and [c] are correct.
Correct Answer: B
Solution :
Here, due to the change in momentum imparted to the sphere, the sphere experiences a force due to incident light. Here, first of all, we see that what is the momentum after reflection in three different cases.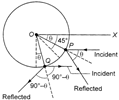 Consider two elements of small area \[\Rightarrow \] at P and Q as shown in the figure. Let, reflection coefficient for the shown case be r. At P, \[\frac{\Delta {{P}_{f}}}{\Delta t}=4\times \frac{l}{C}\times \Delta A\cos 20\] along OX At Q, \[\frac{\Delta {{P}_{f}}}{\Delta t}=r\times \frac{l}{C}\times \Delta A\cos 20\] So, in horizontal direction, rate of change in final momentum is zero and hence due to reflected light force experienced by sphere is zero. In case of perfectly absorbing surface no reflection is there and in this case also, the force experienced by sphere in horizontal direction is only due to incident light. In vertical direction also, the momentum imparted to sphere due to reflected light is zero due to cancellation of lower and upper haves. Thus, we can say that force experienced by sphere is only due to incident light and hence is same in all the three cases, i.e., a and c are wrong. To compute the value of force experienced by the sphere due to incident light we can use the concept of projection, \[{{P}_{1}}=I\times \frac{\pi {{d}^{2}}}{4}\]
Consider two elements of small area \[\Rightarrow \] at P and Q as shown in the figure. Let, reflection coefficient for the shown case be r. At P, \[\frac{\Delta {{P}_{f}}}{\Delta t}=4\times \frac{l}{C}\times \Delta A\cos 20\] along OX At Q, \[\frac{\Delta {{P}_{f}}}{\Delta t}=r\times \frac{l}{C}\times \Delta A\cos 20\] So, in horizontal direction, rate of change in final momentum is zero and hence due to reflected light force experienced by sphere is zero. In case of perfectly absorbing surface no reflection is there and in this case also, the force experienced by sphere in horizontal direction is only due to incident light. In vertical direction also, the momentum imparted to sphere due to reflected light is zero due to cancellation of lower and upper haves. Thus, we can say that force experienced by sphere is only due to incident light and hence is same in all the three cases, i.e., a and c are wrong. To compute the value of force experienced by the sphere due to incident light we can use the concept of projection, \[{{P}_{1}}=I\times \frac{\pi {{d}^{2}}}{4}\]
You need to login to perform this action.
You will be redirected in
3 sec
