question_answer

A point object O is placed in front of a transparent slab at a distance \[x\]from its closer surface. It is seen from the other side of the slab by light incident nearly normally to the slab. The thickness of the slab is t and its refractive index is \[\mu \]. The apparent shift in the position of the object is independent of \[x\] then its value, is

A) \[\left[ 1-\frac{1}{\mu t} \right]\]                    

B) \[\left[ t-\frac{\mu }{t} \right]\]

C) \[t\left[ 1-\frac{t}{\mu } \right]\]                     

D) \[[\mu t-1]\]

Correct Answer: C

Solution :

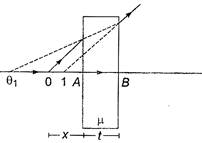The situation is shown in figure. Because of the refraction at the first surface, the image of \[O\] is formed at \[{{O}_{1}}\]. For this refraction, the real depth is \[AO=x\] and the apparent depth is \[A{{O}_{1}}\]. Also, the first medium is air and the second is the slab. Thus,\[\frac{x}{A{{O}_{1}}}=\frac{1}{\mu }\,\]   or         \[A{{O}_{1}}=\mu x\] The point Oi acts as the object for the refraction at the second surface. Due to this refraction, the image of \[{{O}_{1}}\] is formed at \[I\]. Thus, \[\frac{B{{O}_{1}}}{BI}=\mu \] or         \[\frac{AB+B{{O}_{1}}}{BI}=\mu \]         or \[\frac{t+\mu x}{BI}=\mu \] or         \[BI=x+\frac{t}{\mu }\] The net shift is \[OI=OB=\,(x+t)-\,\left( x-\frac{t}{\mu } \right)\] \[=t\,\left( 1-\frac{1}{\mu } \right)\] Which is independent of \[x\].