A) 80 J
B) -180 J
C) 100 J
D) +180 J
Correct Answer: B
Solution :
As the particle is slow shifted, its kinetic energy remains zero. The total work done on the particle is thus zero. The work done by the external agent should be negative of the work done by gravitational field. The work done by the field is \[\int_{i}^{f}{F\cdot \,\,dr}\] Consider figure. Suppose the particle is taken from O to A and then from A to B. The force on the particle is \[F=mE=(2kg)\,(10N/kg)\,(i+j)\] \[=(20N)\,(i+j)\]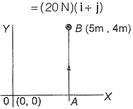 The work done by the field during the displacement OA is \[{{W}_{1}}=\,\int\limits_{5\,m}^{5\,m}{Fx\,dx}\] \[=20\,N\times 5m=100\,J\] Similarly, the work done in displacement AB is \[{{W}_{2}}=\int\limits_{0}^{4\,m}{Fy\,dy=}\,\int\limits_{0}^{4\,m}{(20\,N)\,dy}\] \[\therefore \] \[{{W}_{2}}=80\,\,J\] Thus, the total work done by the field, as the particle is shifted from 0 to 6 is 180 J. Therefore, the work done by the external agent is - 180 J.
The work done by the field during the displacement OA is \[{{W}_{1}}=\,\int\limits_{5\,m}^{5\,m}{Fx\,dx}\] \[=20\,N\times 5m=100\,J\] Similarly, the work done in displacement AB is \[{{W}_{2}}=\int\limits_{0}^{4\,m}{Fy\,dy=}\,\int\limits_{0}^{4\,m}{(20\,N)\,dy}\] \[\therefore \] \[{{W}_{2}}=80\,\,J\] Thus, the total work done by the field, as the particle is shifted from 0 to 6 is 180 J. Therefore, the work done by the external agent is - 180 J.
You need to login to perform this action.
You will be redirected in
3 sec
