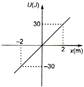
A) Particle is moving along +ve X-axis
B) Particle may move along+ve X-axis
C) Particle may move along -ve X-axis
D) When particle crosses x =-2 m, the speed of particle is \[\sqrt{60}\,m/s\]
Correct Answer: D
Solution :
Here the information about variation of field is given by along X-axis but about \[Y\] and \[Z\]-axis no information is given. On \[Y\] and \[Z\]-coordinate, U may be depending or not. If \[\frac{\partial U}{\partial y}=\frac{\partial U}{az}=0,\], then motion of particle is determined only by From graph, \[{{F}_{x}}=-\frac{\partial U}{\partial x}=-15\,N,\,-ve\] sign shows that \[{{F}_{x}}\] is along \[-ve\] X-axis. Consider two cases ; Case I \[\frac{\partial U}{\partial y}=\frac{\partial U}{\partial z}=0,\] then particle is going to move along -ve X-axis with an acceleration of \[15\,\,m/{{s}^{2}}\] (towards -ve X). Case II \[\frac{\partial U}{\partial y}\] and/or \[\frac{\partial U}{\partial z}\ne 0,\]. then particle's motion cannot be exactly determined from given information but it is for sure that in any circumstance, the particle won't move along +ve X-axis, So, particle may move in -ve X-axis. From work energy theorem \[dK=-dU\] \[\Rightarrow \] \[\frac{m{{v}^{2}}}{2}-0=-\{[-30+{{U}_{y}}+{{U}_{z}}]\,-{{[u]}_{0,\,0,\,0}}\}\] \[v=\sqrt{60}\,m/s\] if U is not depending on y and z.You need to login to perform this action.
You will be redirected in
3 sec
