question_answer

Direction: Light having photons energy \[hv\] is incident on a metallic plate having work function \[\phi \] to eject the electrons.

The most energetic electrons are then allowed to enter in a region of uniform magnetic field B as shown in the figure.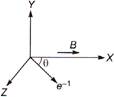

The electrons are projected in XZ-plane making an angle of\[\theta \] with X-axis and magnetic field is \[\mathbf{B}={{B}_{0}}\,i\] along X-axis. Maximum pitch of the helix described by electron is found to be p. Take mass of electron as m and charge as q. Based on above information, answer the following questions

The correct relation between P and \[{{B}_{0}}\] is

A)  \[qP{{B}_{0}}=2\pi \,\cos \,\theta \,\sqrt{2\,(hv-\phi )\,m}\]

B)  \[qP{{B}_{0}}=2\pi \,\cos \,\theta \,\sqrt{\frac{2\,(hv-\phi )}{m}}\]

C)  \[qP{{B}_{0}}=2\pi \,\sqrt{2\,(hv-\phi )\,m}\,\]

D)  \[P=\frac{2gm}{q{{B}_{0}}}\times \sqrt{hv-\phi }\]

Correct Answer: A

Solution :

 At any time rthe location of electron is shown as P. In two dimensional view of electron in YZ-plane, the situation is more clear.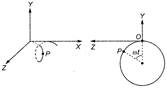 As we kow that for photoelectron, \[\frac{1}{2}\,m{{v}^{2}}=hv-\phi \] \[\Rightarrow \]            \[v=\sqrt{\frac{2(hv-\phi )}{m}}\] And time period of change in magnetic field, \[T=\frac{2\pi m}{qB}\] \[\therefore \] Pitch, P = advance in on time period \[v=\,\,\cos \,\,\theta \times t\] \[\sqrt{\frac{2(hv-\phi )}{m}}\times \,\cos \,\theta \,\times \frac{2\pi m}{qB}\] \[\Rightarrow \]            \[Pq{{B}_{0}}=2\pi \,\cos \,\theta \,\sqrt{2m(hv-\phi )}\]