| Direction: Light having photons energy \[hv\] is incident on a metallic plate having work function \[\phi \] to eject the electrons. |
The most energetic electrons are then allowed to enter in a region of uniform magnetic field B as shown in the figure. 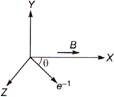 |
| The electrons are projected in XZ-plane making an angle of\[\theta \] with X-axis and magnetic field is \[\mathbf{B}={{B}_{0}}\,i\] along X-axis. Maximum pitch of the helix described by electron is found to be p. Take mass of electron as m and charge as q. Based on above information, answer the following questions |
A) \[-\frac{-\sqrt{2m\,(hv-\phi )}}{q{{B}_{0}}}\sin \,\theta \,\left[ 1-\cos \,\left( \frac{q{{B}_{0}}t}{m} \right) \right]\]
B) \[\frac{\sqrt{2m\,(hv-\phi )}}{q{{B}_{0}}}\sin \,\theta \,\times \sin \,\left[ \frac{q{{B}_{0}}t}{m} \right]\]
C) \[\frac{-\sqrt{2m\,(hv-\phi )}}{q{{B}_{0}}}\sin \,\theta \,\times \sin \,\left[ \frac{q{{B}_{0}}t}{m} \right]\]
D) \[\frac{\sqrt{2m\,(hv-\phi )}}{q{{B}_{0}}}\times \sin \,\left( \frac{q{{B}_{0}}t}{m} \right)\]
Correct Answer: B
Solution :
\[X-\]coordinate, \[x=v\,\,\cos \,\,\theta \times t\] \[Y-\]coordinate, \[y=-[R-R\,\cos \,\omega t]\] Z-coordinate, \[z=R\,\sin \,\omega t\] \[z=\frac{mv\,\sin \,\theta }{q{{B}_{0}}}\times \sin \,\left[ \frac{q{{B}_{0}}}{m}t \right]\] \[=\sqrt{\frac{2m(hv-\phi )\times \,sin\,\theta }{q{{B}_{0}}}}\times \sin \,\left[ \frac{q{{B}_{0}}t}{m} \right]\] As v increases, slope of \[x\] versus \[t\] graph (a straight line increases).You need to login to perform this action.
You will be redirected in
3 sec
