question_answer

A circle concentric to the ellipse \[\frac{4{{x}^{2}}}{289}+\frac{{{y}^{2}}}{{{k}^{2}}}=1,\] where \[k<\frac{17}{2},\] passes through foci \[{{S}_{1}}\] and\[{{S}_{2}}\] of the ellipse and cuts ellipse at point P. If area of \[\Delta P{{S}_{1}}{{S}_{2}}\] is 35 sq units, then \[{{S}_{1}}{{S}_{2}}\] is equal to

A)  12 units                      

B)  13 units           

C)  \[\sqrt{149}\] units                

D)  \[\sqrt{49}\] units

Correct Answer: C

Solution :

 Since, circle is concentric to the ellipse and passes through the foci \[{{S}_{1}}\] and \[{{S}_{2}}\].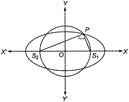 Hece, \[{{S}_{1}}{{S}_{2}}\] in the diameter of the circle. Then, area of \[\Delta P{{S}_{1}}{{S}_{2}}\] \[=\frac{1}{2}\,({{S}_{1}}P)\,({{S}_{2}}P)\] as \[{{S}_{1}}{{S}_{2}}\] is daimeter But,      \[{{S}_{1}}P+{{S}_{2}}P=2a=17,\] then Area \[=\frac{1}{2}\,x\,(17-x)\,=35,\] where \[{{S}_{1}}P=x\] \[\Rightarrow \]            \[{{x}^{2}}-17x+70=0\] \[\Rightarrow \]            \[x=7,\,\,10\] \[\therefore \]    \[{{S}_{1}}{{S}_{2}}\,\sqrt{PS_{1}^{2}+PS_{2}^{2}}\] \[=\sqrt{49+100}\] \[=\sqrt{149}\]            units