question_answer

Let the length of the tangent drawn from a variable point to one. given circle is\[\mu \,(\mu \ne 1)\]times the length of the tangent from it to another circle. The locus of the variable point is

A)  a circle                       

B)  a parabola        

C)  a straight line             

D)  a hyperbola

Correct Answer: A

Solution :

 We have, \[P{{T}_{1}}=\mu P{{T}_{2}}\]    (by condition)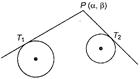 \[\Rightarrow \]            \[{{\alpha }^{2}}+{{\beta }^{2}}+2{{g}_{1}}\alpha +2{{f}_{1}}\beta +{{c}_{1}}\] \[={{\mu }^{2}}\,({{\alpha }^{2}}+{{\beta }^{2}}+2{{g}_{2}}\alpha +2{{f}_{2}}\beta +{{c}_{2}})\] Hence, locus of \[(\alpha ,\,\,\beta )\] is \[({{x}^{2}}+{{y}^{2}})\,({{\mu }^{2}}-1)+2({{g}_{2}}{{\mu }^{2}}-{{g}_{1}})x\] \[+2\,({{f}_{2}}{{\mu }^{2}}-{{f}_{1}})\,y+{{c}_{2}}{{\mu }^{2}}-{{c}_{1}}=0\] Which is a circle.