question_answer

The distances of a point (7, -3) from the foci of the ellipse \[3{{x}^{2}}+4{{y}^{2}}-12x+24y+36=0\]are 'a' and 'b' respectively, then a and b satisfy

A)  \[a+b=10\]               

B)  \[a+b=6\]

C) \[|b-a|\,=\,14\]                

D)  \[|a\pm b|\,=\,2009\]

Correct Answer: A

Solution :

 The equation of the ellipse can be written as \[\frac{{{(x-2)}^{2}}}{4}+\frac{{{(y+3)}^{2}}}{3}=1,\] whose centre is (2, -3) and vertices are \[A(4,\,\,-3)\] and \[A'(0,\,-3)\] foci are \[S(3,-3)\] and \[S'(1,-3)\]. \[\left( \because \,\,e=\frac{1}{2} \right)\]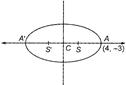 a = Distance between P(7, -3) and S (3, -3) = 4 and b = distance between P(7, - 3) and S? (1, -3) = 6 \[\therefore \]    \[a+b=4+6=10\]