question_answer

Direction: For the following questions. Choose the correct answer from the codes [a], [b], [c] and [d] defined as follows.

For each of the following questions, one out of given options is correct.

Statement I lf\[\frac{x}{a}+\frac{y}{b}=1\] and \[\frac{x}{c}+\frac{y}{d}=-1\] cut \[x\] and \[y-\] axes at four concyclic points, A, B, C and D respectively, then the orthocentre of \[\Delta ABC\]is \[\left( 0,\,\frac{ac}{b} \right)\].

Statement II If chords AC and BD of a circle intersect at origin O, then\[OA\cdot OC=OB\cdot OD\].

A)  Statement I is true, Statement II is also true and Statement II is the correct explanation of Statement I.

B)  Statement I is true. Statement II is also true and Statement II is not the correct explanation of Statement I.

C)  Statement I is true, Statement II is false.

D)  Statement I is false. Statement II is true.

Correct Answer: B

Solution :

 The orthocentre of \[\Delta ABC\] be \[H(0,\,\,\alpha )\]. \[\Rightarrow \]            \[{{m}_{CH}}\cdot {{m}_{AB}}=-1\] \[\Rightarrow \]            \[\frac{\alpha -0}{0-(-c)}\cdot \,\frac{b-0}{0-a}=-1\] \[\Rightarrow \]            \[b\alpha =ac\] \[\Rightarrow \]            \[\alpha =\frac{ac}{b}\] \[\therefore \] Orthocentre of \[\Delta ABC\] is \[H\left( 0,\,\frac{ac}{b} \right)\].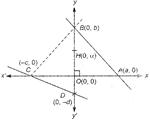 Also, statement II is true but not the correct explanation for statement I.