question_answer

A circular arc AB of thin wire frame of radius R and mass M makes an angle of \[90{}^\circ \] at the origin. The centre of mass of the arc lies at

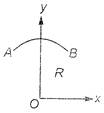
A)  \[\left[ 0,\,\left( \frac{2}{\pi } \right)R \right]\]            

B)  \[\left[ 0,\,\left( \frac{\sqrt{2}}{\pi } \right)R \right]\]

C)  \[\left[ 0,\,\left( \frac{2\sqrt{2}}{\pi } \right)R \right]\]

D)  \[\left[ 0,\,\left( \frac{4}{\pi } \right)R \right]\]

Correct Answer: C

Solution :

 By symmetry, \[{{X}_{CM}}=0\] As,       \[dm=\lambda R\,\,d\theta \]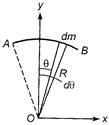 \[\therefore \]    \[{{y}_{CM}}=\frac{\int{y\,\,dm}}{\int{dm}}=\frac{1}{m}\,\int{R\,\cos \,\theta \lambda R\,\,d\theta }\] \[=\frac{{{R}^{2}}\lambda }{m}\int_{-\pi 4}^{\pi /4}{\cos \,\theta \,d\theta }\] \[=\frac{{{R}^{2}}\lambda }{R\times \lambda \times \left( \frac{\pi }{2} \right)}\left[ 2\,\sin \,\frac{\pi }{4} \right]\] \[=\frac{2R}{\pi }\,2\frac{1}{\sqrt{2}}=\frac{2\sqrt{2}\,R}{\pi }\]