A) \[\frac{\sqrt{3}}{4}\frac{{{l}^{2}}}{R}\]
B) \[\frac{4}{\sqrt{3}}\frac{{{l}^{2}}}{R}\]
C) \[\frac{\sqrt{3}}{4}\frac{R}{{{l}^{2}}}\]
D) \[\frac{4}{\sqrt{3}}\frac{R}{{{l}^{2}}}\]
Correct Answer: A
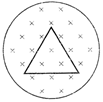
Solution :
With the help of information?s in the equation. \[\phi =\frac{\sqrt{3}}{4}{{I}^{2}}B,\,\,\Rightarrow \,\,\varepsilon =\left| \frac{d\phi }{dt} \right|=\frac{\sqrt{3}}{4}{{I}^{2}}\,\frac{dB}{dt},\] \[\therefore \] \[I=\frac{\pi }{R}=\,\frac{\sqrt{3}{{I}^{2}}}{4R}\]You need to login to perform this action.
You will be redirected in
3 sec
