question_answer

Drops of liquid of density d are floating half immersed in a liquid of density \[\rho \]. If the surface tension of liquid is T, then radius of the drop will be

A)  \[\sqrt{\frac{3T}{g(2d-\rho )}}\]       

B)  \[\sqrt{\frac{3T}{g(d-\rho )}}\]

C)  \[\sqrt{\frac{6T}{g(2d-\rho )}}\]       

D)  \[\sqrt{\frac{6T}{g(d-\rho )}}\]

Correct Answer: A

Solution :

 For equilibrium of drop, \[\frac{2}{3}\pi {{R}^{3}}\,\rho g+2\pi RT=\frac{4}{3}\pi {{R}^{3}}dg\]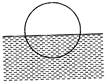 \[\Rightarrow \]            \[2RT=\frac{2}{3}{{R}^{3}}g\,(2d-\rho )\] \[\therefore \]    \[R=\sqrt{\frac{3T}{(2d-\rho )g}}\]