| Direction: A voltage source \[V={{V}_{0}}\,\sin \,(100t)\] is connected to a black box in which there can he either one element out of L, C, R or any two of them connected in series. |
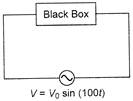 |
| At steady state the variation of current in the circuit and the source voltage are plotted together with time, using an oscilloscope, as shown. |
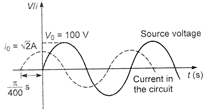 |
A) \[R=50\,\Omega ,\,\,C=200\,\mu F\]
B) \[R=50\,\Omega ,\,\,L=2\,m\mu \]
C) \[R=400\,\Omega ,\,C=50\,\mu F\]
D) \[R=50\,\Omega ,\,\,L=02H\]
Correct Answer: A
Solution :
\[\Delta \theta =\omega \Delta t=\frac{\pi }{4}\] \[\tan \,\theta =\frac{X}{R}\] \[\Rightarrow \] \[X=R\] Since, current leads the voltage the circuit consists of R and C. and \[{{i}_{0}}=\frac{{{V}_{0}}}{z}\] \[\therefore \] \[z=\frac{{{V}_{0}}}{{{i}_{0}}}=\frac{100}{\sqrt{2}}=50\sqrt{2}\] Now, \[R\sqrt{2}=50\sqrt{2}\] \[\Rightarrow \] \[R={{X}_{C}}=50\] \[{{X}_{C}}=\frac{1}{C\omega }=50\] \[\Rightarrow \] \[C=\frac{1}{50\,\omega }=200\,\mu F\] \[\tau =RC=50\times 200\times {{10}^{-6}}=1\times {{10}^{-2}}s\]You need to login to perform this action.
You will be redirected in
3 sec
