A) \[\left( \frac{-1}{2},\,0 \right)\]
B) \[\left( \frac{-1}{2},\,2 \right)\]
C) \[\left( \frac{-1}{2},\,-2 \right]\]
D) \[\left( \frac{1}{2},\,\infty \right)\]
Correct Answer: A
Solution :
\[\because \] \[f(x)=|x|-\{x\}\]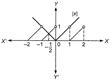 \[\because \] \[f(x)\] is decreasing. \[\therefore \] \[f'(x)<0\] \[\Rightarrow \] \[|x|-\{x\}<0\] \[\Rightarrow \] \[|x|\,<\{x\}\] From figure, \[x\in \,\left( -\frac{1}{2},\,\,0 \right)\] From graph, it is clear that, \[f(x)\] has local maxima at \[x=1\].
\[\because \] \[f(x)\] is decreasing. \[\therefore \] \[f'(x)<0\] \[\Rightarrow \] \[|x|-\{x\}<0\] \[\Rightarrow \] \[|x|\,<\{x\}\] From figure, \[x\in \,\left( -\frac{1}{2},\,\,0 \right)\] From graph, it is clear that, \[f(x)\] has local maxima at \[x=1\].
You need to login to perform this action.
You will be redirected in
3 sec
