A) \[\sqrt{g\ell }\]
B) \[\sqrt{3g\ell /5}\]
C) \[\sqrt{2g\ell /5}\]
D) No such condition is possible
Correct Answer: A
Solution :
Let u is the speed of particle (bob) when it is at mean position and v when it is making an angle of \[37{}^\circ \] with the vertical.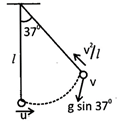 For given condition, \[g\sin 37=\frac{{{v}^{2}}}{\ell }\] \[\Rightarrow \]\[{{v}^{2}}=g\ell \times \frac{3}{5}=\frac{3g\ell }{5}\] From work energy theorem \[\frac{m{{u}^{2}}}{2}=\frac{m{{v}^{2}}}{2}=mg\times \ell (1-cos37)=\frac{mg\ell }{5}\] \[\Rightarrow \]\[{{u}^{2}}={{v}^{2}}+\frac{2g\ell }{5}=\frac{3g\ell }{5}+\frac{2g\ell }{5}=a\ell \]
For given condition, \[g\sin 37=\frac{{{v}^{2}}}{\ell }\] \[\Rightarrow \]\[{{v}^{2}}=g\ell \times \frac{3}{5}=\frac{3g\ell }{5}\] From work energy theorem \[\frac{m{{u}^{2}}}{2}=\frac{m{{v}^{2}}}{2}=mg\times \ell (1-cos37)=\frac{mg\ell }{5}\] \[\Rightarrow \]\[{{u}^{2}}={{v}^{2}}+\frac{2g\ell }{5}=\frac{3g\ell }{5}+\frac{2g\ell }{5}=a\ell \]
You need to login to perform this action.
You will be redirected in
3 sec
