A) \[\frac{1}{3}\]
B) \[\frac{2}{3}\]
C) 1
D) \[\frac{3}{2}\]
Correct Answer: B
Solution :
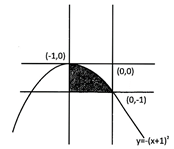 \[-\frac{\pi }{2}\le {{\sin }^{-1}}x\le \frac{\pi }{2}-\frac{\pi }{2}\le {{\sin }^{-1}}y\le \frac{\pi }{2}\] \[-\pi \le {{\sin }^{-1}}x+{{\sin }^{-1}}y\le \pi \] So for\[{{\sin }^{-1}}x+{{\sin }^{-1}}y=-\pi \] \[\Rightarrow \]\[{{\sin }^{-1}}x=-\frac{\pi }{2}\And si{{n}^{-1}}y=-\frac{\pi }{2}\]x = - and y = - 1 area required \[=1-\left| \int\limits_{-1}^{0}{-{{(x+1)}^{2}}dx} \right|\] \[=1-\frac{1}{3}=\frac{2}{3}\]sq. units.
\[-\frac{\pi }{2}\le {{\sin }^{-1}}x\le \frac{\pi }{2}-\frac{\pi }{2}\le {{\sin }^{-1}}y\le \frac{\pi }{2}\] \[-\pi \le {{\sin }^{-1}}x+{{\sin }^{-1}}y\le \pi \] So for\[{{\sin }^{-1}}x+{{\sin }^{-1}}y=-\pi \] \[\Rightarrow \]\[{{\sin }^{-1}}x=-\frac{\pi }{2}\And si{{n}^{-1}}y=-\frac{\pi }{2}\]x = - and y = - 1 area required \[=1-\left| \int\limits_{-1}^{0}{-{{(x+1)}^{2}}dx} \right|\] \[=1-\frac{1}{3}=\frac{2}{3}\]sq. units.
You need to login to perform this action.
You will be redirected in
3 sec
