A) \[\frac{{{T}_{1}}}{{{T}_{2}}}=\frac{1}{2}\]
B) \[\frac{{{T}_{1}}}{{{T}_{2}}}=\frac{2}{1}\]
C) \[\frac{{{T}_{1}}}{{{T}_{2}}}=\frac{1}{\sqrt{2}}\]
D) \[\frac{{{T}_{1}}}{{{T}_{2}}}=\frac{\sqrt{2}}{1}\]
Correct Answer: B
Solution :
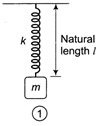
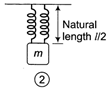
Idea If a spring having spring constant k is divided into n equal parts, then the spring constant of each part will become nk. Case I\[{{T}_{1}}=2\pi \sqrt{\frac{m}{k}}\] When the spring is cut into two equal parts, then spring constant for each part will become double. \[\Rightarrow \]\[k'=2k\] Case II \[{{k}_{eq}}=2k+2k=4k\] (parallel) So, \[{{T}_{2}}=2\pi \sqrt{\frac{m}{4k}}\] \[{{T}_{2}}=\frac{2\pi }{2}\sqrt{\frac{m}{4k}}\]\[\Rightarrow \]\[\frac{{{T}_{1}}}{{{T}_{2}}}=\frac{2}{1}\] TEST Edge Question related to cutting of spring, changing the length of spring can be asked in the examination. Following point will be useful from examination point of view. If length of the spring in made n times then effective force constant becomes\[\frac{1}{n}\]times and time period become\[\sqrt{n}\]times. In horizontal spring mass oscillation the mean position is when the spring is unstretched (uncompressed). In vertical spring mass oscillation the mean position will be at a stretch of\[x=\frac{mg}{\kappa }\]. If we just left a spring-mass system vertically.You need to login to perform this action.
You will be redirected in
3 sec
