At steady state the variation of current in the circuit and the source voltage are plotted together with time, using an oscilloscope as shown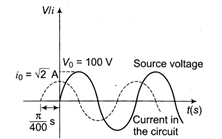 
If AC source is removed, the circuit is shorted and then at t = 0, a battery of constant emf is connected across the black box. The current in the circuit will
A) increase exponentially with constant\[4\times {{10}^{-3}}\]s
B) decrease exponentially with time constant\[1\times {{10}^{-2}}\]
C) oscillate with angular frequency\[20\,{{s}^{-1}}\]
D) first increase and then decrease
Correct Answer: B
Solution :
\[\Delta \theta =\omega \Delta t=\frac{\pi }{4}\] \[\tan \theta =\frac{X}{R}\] \[\Rightarrow \]\[X=R\] Since, current leads the voltage the circuit consists of R and C, and\[{{i}_{0}}=\frac{{{V}_{0}}}{Z}\] \[\therefore \]\[Z=\frac{{{V}_{0}}}{{{i}_{0}}}=\frac{100}{\sqrt{2}}=50\sqrt{2}\] Now, \[R\sqrt{2}=50\sqrt{2}\Rightarrow R={{X}_{C}}=50\] \[{{X}_{C}}=\frac{1}{C\omega }=50\] \[\Rightarrow \]\[C=\frac{1}{50\omega }=200\mu F\] \[\tau =RC=50\times 200\times {{10}^{-6}}=1\times {{10}^{-2}}\]s
You need to login to perform this action.
You will be redirected in
3 sec
