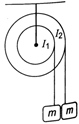
A) \[{{\omega }_{1}}={{\omega }_{2}}\]
B) \[{{\omega }_{1}}>{{\omega }_{2}}\]
C) \[{{\omega }_{1}}<{{\omega }_{2}}\]
D) Information insufficient
Correct Answer: D
Solution :
Idea Here, pulleys will rotate due to the tension of rope as pulleys are rough. The angular speeds will depend on the angular acceleration. So, just find angular acceleration to find relation between\[{{\omega }_{1}}\]and\[{{\omega }_{2}}\]. As, \[\omega ={{\omega }_{0}}+\alpha t\] Since, \[{{\omega }_{0}}=0\]so, \[\omega =\alpha t\] So, the pulley which has more angular acceleration would have more angular velocity. Now, consider a pulley mass system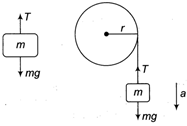 \[ma=mg-T\] \[\Rightarrow \]\[a=g-T/m\]...(i) Since, \[a=\alpha .r\] and as\[l\alpha =T\times r\] i.e., \[\alpha =\frac{Tr}{l}\] \[\therefore \]\[a=\frac{T{{r}^{2}}}{l}\] \[\Rightarrow \]\[\frac{T.{{r}^{2}}}{l}=g-\frac{T}{m}\] \[\Rightarrow \]\[T\left[ \frac{1}{m}+\frac{{{r}^{2}}}{l} \right]=g\] \[\Rightarrow \]\[T=\frac{g}{\frac{1}{m}+\frac{{{r}^{2}}}{l}}\] \[\therefore \]\[\alpha =\frac{gr}{\left( \frac{1}{m}+\frac{{{r}^{2}}}{l} \right)l}=\frac{mgr}{l+m{{r}^{2}}}\] Since, relation between r2/l is not given. So, data is insufficient here. TEST Edge
\[ma=mg-T\] \[\Rightarrow \]\[a=g-T/m\]...(i) Since, \[a=\alpha .r\] and as\[l\alpha =T\times r\] i.e., \[\alpha =\frac{Tr}{l}\] \[\therefore \]\[a=\frac{T{{r}^{2}}}{l}\] \[\Rightarrow \]\[\frac{T.{{r}^{2}}}{l}=g-\frac{T}{m}\] \[\Rightarrow \]\[T\left[ \frac{1}{m}+\frac{{{r}^{2}}}{l} \right]=g\] \[\Rightarrow \]\[T=\frac{g}{\frac{1}{m}+\frac{{{r}^{2}}}{l}}\] \[\therefore \]\[\alpha =\frac{gr}{\left( \frac{1}{m}+\frac{{{r}^{2}}}{l} \right)l}=\frac{mgr}{l+m{{r}^{2}}}\] Since, relation between r2/l is not given. So, data is insufficient here. TEST Edge 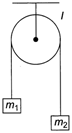 Rough pulley-block system could also be solved by applying conservation of mechanical energy. \[\Delta KE+\Delta PE=0\]
Rough pulley-block system could also be solved by applying conservation of mechanical energy. \[\Delta KE+\Delta PE=0\]
You need to login to perform this action.
You will be redirected in
3 sec
