A) \[\frac{a{{t}^{2}}}{3}\]
B) \[\frac{a{{t}^{2}}}{2}\]
C) \[a{{t}^{2}}\]
D) \[\frac{a{{t}^{2}}}{4}\]
Correct Answer: A
Solution :
Idea It is a simple question based on kinematics equations. First apply the equation for acceleration and then for retardation. Let, \[{{t}_{0}}\]is the time during acceleration then\[\frac{{{t}_{0}}}{2}\]will be the time of de-acceleration in order to bring car to rest again. So, time of journey\[t={{t}_{0}}+\frac{{{t}_{0}}}{2}=\frac{3{{t}_{0}}}{2}\] \[\therefore \]\[{{t}_{0}}=\frac{2t}{3}\] and\[\frac{{{t}_{0}}}{2}=\frac{t}{3}\] Hence, \[s=\frac{1}{2}a\times {{({{t}_{0}})}^{2}}+\frac{1}{2}\times 2a\times {{\left( \frac{{{t}_{0}}}{2} \right)}^{2}}\] \[=\frac{1}{2}a{{\left( \frac{2t}{3} \right)}^{2}}+\frac{1}{2}2a\times {{\left( \frac{t}{3} \right)}^{2}}=\frac{a{{t}^{2}}}{3}\] TEST Edge In kinematics different types of questions could be asked, e.g., if a body is in free fall draw the graph between\[{{v}^{2}}\]and s (reference point could be considered at any point). Let us consider origin at the highest point from where we have left the object. For free fall, \[{{v}^{2}}={{u}^{2}}+2as\] \[\therefore \]\[u=0\] \[{{v}^{2}}=2as\] \[{{v}^{2}}/s=2a=\]constant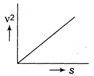
You need to login to perform this action.
You will be redirected in
3 sec
